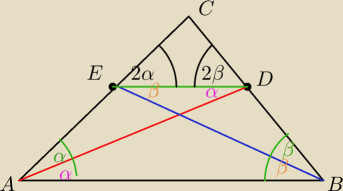
Trojkat 6latek: W trojkacie ABC dwusieczne kątow A i B przecinaja przeciwlegle boki w punktach D i E tak ze DEIIAB Wykaz ze trojkat ABC jest rownoramienny Do czego doszedlem Kąty α i β jako kąty naprzemianlegle wewnetrzne Oznacza to ze ΔEAD i ΔDEB sa rownoramienne Kąty 2α i 2β jako kąty odpowiadajace Teraz by nalezalo pokazac ze AD=BE

wredulus_pospolitus: Wiemy, że |AE| = |BD| = k (patrz wskazane trójkąty równoramienne) z tw. Talesa:

|EC|		|DC|		|EC|		|BC|
	=		⇔		=
|AC|		|BC|		|EC| + k		|BC|+k

na krzyż |EC|*|BC| + k|EC| = |EC|*|BC| + k|BC| ⇔ |EC| = |BC| c.n.w.

wredulus_pospolitus:

	|EC|		|DC|
błąd w zapisie przy równaniu ... winno być :		=
	|EC| + k		|DC| + k

i tak samo później po wymnożeniu

6latek: Dziekuje Ci Prosze abys sie moze pochylil nad tym co ja probowalem wymlodszic z katow i przystawania trojkatow

wredulus_pospolitus: Pochyliłem się i szczerze mówiąc ... nie wiem jak wykazać |AD| = |BE| na tym etapie (gdy nie wiesz czy α=β) Po prostu, nie widzę tutaj sposobu na wykazanie tego na tym etapie.

wredulus_pospolitus: Dobra ... wiem (chyba) Zauważ, że ABDE to trapez ... własnie pokazaliśmy, że jest to trapez równoramienny Opuszczamy wysokości z D i E (punkty na AB nazwijmy D' i E' ). Jako, że trapez jest równoramienny to więc |AD'| = |BE'| wysokości oczywiście te same (daaa) na mocy tw. Pitagorasa −> przekątne trapezu są sobie równe

wredulus_pospolitus: Chociaż to i tak było niepotrzebne ... bo skoro mamy trapez równoramienny ... to kąty przy podstawach są sobie równe ... więc 2α = 2β więc ABC jest równoramienny.

6latek: Dziekuje . Ogladalem kwalifikacje w skokach

6latek: Moze ktos jeszce sie pochyli nad tym ?

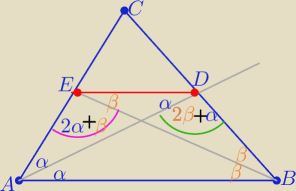
Eta: ABDE jest trapezem bo AB ∥DE 2α+2α+β+β =180^o i 2β+2β+α+α =180^o ⇒ 2α=2β co daje tezę Δ ABC jest równoramienny

6latek: W pierwszej chwili nie pomyslalem o trapezie czyli wredulus tez mial racje piszac o trapezie Dzieki wiekie