wykaż, że Julia: Dany jest równoległobok ABCD, w którym bok AB jest dwa razy dłuższy od boku BC. W połowie odcinka AB zaznaczono punkt K. Wykaż, że kąt DKC jest kątem prostym

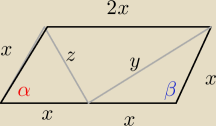
wredulus_pospolitus: β = 180 − α więc cosβ = cos(180 − α) = −cosα z tw. cosinusów: z² = x² + x² − 2x²cosα y² = x² + x² − 2x²cosβ = x² + x² +2x²cosα więc (dodajemy te równania): z² + y² = 4x² = (2x)² i otrzymujemy tw. Pitagorasa

PW: Dowód elementarny, wykorzystujący załozenie o punkcie K Punkt K dzieli AB na pół, a więc trójkąty CKB i DKA są równoramienne, wobec tego

	180°−β		β
∡CKB =		= 90°−		,
	2		2

podobnie

	α
∡DKA = 90°−
	2

Ponieważ ∡DKA + ∡DKC + ∡CKB = 180°, z (1), (2) podstawionych do (3) wynika

	α		β
90°−		+ ∡DKC + 90°−		= 180°,
	2		2

a więc

	α+β
∡DKC =		;
	2

jest oczywiste, że α+β = 180°, zatem

	180°
∡DKC =		= 90°,
	2

co należało wykazać.

PW: Julio, tyś ta sama, co niedawno pytała o całki, czy jesteś swoją młodszą siostrą?

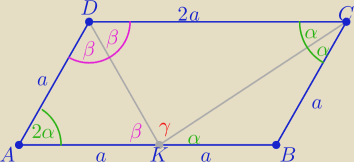
Eta: 2α+2β=90^o ⇒ α+β=90^o i α+β+γ=180^o to γ=90^o Δ DKC jest prostokątny c.n.w.

dofs: Eta, wkradł się mały błąd, mianowicie ''2α+2β=90°'', gdzie powinno być ''2α+2β=180°''

6latek: Dzien dobry Znowu dokuczasz PW

PW: Nie, wcale mi nie dokucza. Po prostu wykonała ładny ysunek. Szkoda tylko, że zmieniła oznaczenia wredulusa, których sie trzymałem. Dowód Ety w gruncie rzeczy jest taki sam − polega na zauważeniu dwóch trójkątów równoramiennych.

6latek: To byl żart Ale za to ja mam 3 rozwiazania tego zadania