funkcje adnt: Wykres funkcji liniowej przechodzi przez punkt A= (−1, 3) i ma dokładnie jeden punkt wspólny z parabola o równianiu y=−x². Znajdź wzór funkcji f

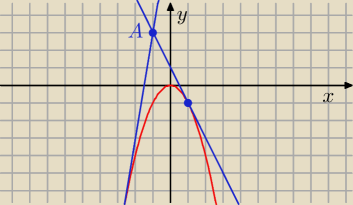
janek191: y = a x + b A = ( −1 , 3) 3 = − a + b ⇒ b = a + 3 y = a x + a + 3 więc a x + a + 3 = −x² x² + a x + a + 3 = 0 Δ = a² − 4*1*(a + 3) = a² − 4 a − 12 = 0 Δ_a = 16 − 4*1*(−12) = 16 + 48 = 64 √Δ_a = 8

	4 − 8
a =		= − 2 lub a = 6
	2

więc b = 1 lub b = 9 Odp. y = −2 x + 1 lub y = 6 x + 9 =============================

adnt: janek191 można byłoby wyliczyć to za pomocą pochodnej?

PW: Ano nie można, i tu widać doświadczenie Janka191. Określenia "prosta ma jeden punkt wspólny z parabolą" i "prosta jest styczna do paraboli" nie są synonimami. Posługując się pochodną uzyskałbyś tylko równanie stycznej y = −2x+1.

wredulus_pospolitus: PW f(x) = −x² f'(x) = −2x y − f(x₀) = f'(x_o)*(x−x_o) y + x_o² = −2x_o(x−x_o) y = −2x*x_o + x_o² <−−− ogólna postać stycznej (zalezna od punktu styczności) podstawiamy współrzędne punktu A. 3 = −2*(−1)*x_o + x_o² 3 = 2x_o + x_o² x_o = 1 lub x_o = −3 i wracamy do wzoru stycznej: 1) y = −2x + 1 2) y = 6x + 9 Więc tak ... dostaniemy dwie styczne. Należy zauważyć, że w ogólnym przypadku. prosta będzie miała z parabola tylko jeden punkt wspólny gdy: 1) Jest styczna do tejże paraboli (wyznaczyliśmy obie styczne) 2) Jest osią symetrii tejże paraboli (co w naszym przypadku jest niemożliwe) W każdym innym przypadku albo przetnie dwukrotnie parabolę albo wcale.

PW: Masz rację, coś mi się uroiło. Tak to jest gdy zamiast policzyć patrzy się na rysunek. Ale podtrzymuję, że rozwiązanie Janka191 jest ładne (przecież nie pytali o styczne, lecz o wykresy funkcji liniowej mające jeden punkt wspólny z parabolą). Te inne "nie styczne, ale mające jeden punkt wspólny" muszą być pionowe.

wredulus_pospolitus: Fakt ... pionowe ...nie muszą być osią symetrii ... ale w tym konkretnym przypadku nie są rozwiązaniami ... bo to nie są funkcje, a pytanie było o funkcje