 Zadanie 5.
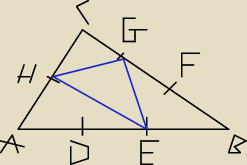
W trójkącie 𝐴𝐵𝐶 punkty 𝐷, 𝐸 dzielą bok 𝐴𝐵 na trzy odcinki równej długości; punkty 𝐹, 𝐺
dzielą
bok 𝐵𝐶 na trzy odcinki równej długości, a punkt 𝐻 jest środkiem boku 𝐴𝐶 (zobacz rysunek).
Oblicz
jaką część pola trójkąta 𝐸𝐺𝐻 stanowi pole trójkąta 𝐴𝐵𝐶.
Mógłby mi ktoś ogarnąć to zadanie bez sinusów?
Zadanie 5.
W trójkącie 𝐴𝐵𝐶 punkty 𝐷, 𝐸 dzielą bok 𝐴𝐵 na trzy odcinki równej długości; punkty 𝐹, 𝐺
dzielą
bok 𝐵𝐶 na trzy odcinki równej długości, a punkt 𝐻 jest środkiem boku 𝐴𝐶 (zobacz rysunek).
Oblicz
jaką część pola trójkąta 𝐸𝐺𝐻 stanowi pole trójkąta 𝐴𝐵𝐶.
Mógłby mi ktoś ogarnąć to zadanie bez sinusów? 
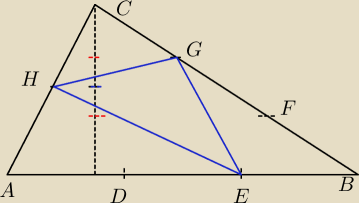 Zauważ, że pole szukanego trójkąta to nic innego jak:
PABC − P{AEH} − P{EBG} − P{HGC}
zauważ, że na wysokości ΔABC zaznaczyłem przerywanymi liniami pewne miejsca ... korzystając z
tw. Talesa mogę wykazać, że czerwone wartości wyznaczają punkty które dzielą wysokość na
3 równe części (a odcinki łączące je z odpowiednią G i F będzie będą RÓWNOLEGŁE do podstawy
AB)
natomiast niebieski punkt dzieli wysokość na pół i tak 'jest na wysokości' punktu H
Tak więc stąd wiemy, że:
Zauważ, że pole szukanego trójkąta to nic innego jak:
PABC − P{AEH} − P{EBG} − P{HGC}
zauważ, że na wysokości ΔABC zaznaczyłem przerywanymi liniami pewne miejsca ... korzystając z
tw. Talesa mogę wykazać, że czerwone wartości wyznaczają punkty które dzielą wysokość na
3 równe części (a odcinki łączące je z odpowiednią G i F będzie będą RÓWNOLEGŁE do podstawy
AB)
natomiast niebieski punkt dzieli wysokość na pół i tak 'jest na wysokości' punktu H
Tak więc stąd wiemy, że:
| 1 | 2 | 1 | 1 | |||||
P(AEH} = | * | |AB|* | h = | PABC | ||||
| 2 | 3 | 2 | 3 |
| 1 | 1 | 2 | 2 | |||||
PEBG = | * | |AB|* | h = | PABC | ||||
| 2 | 3 | 3 | 9 |