Oblicz dlugosci przekatnych rombu Ika: Dany jest romb ABCD. Wiedząc, że kąt ostry rombu ma miarę 30°, a promień okręgu wpisanego w romb jest równy 4, oblicz długości przekątnych tego rombu oraz jego obwód. Wysokość rombu poprowadzona przez punkt przecięcia przekątnych dzieli bok rombu na odcinki mające długość 9 𝑐𝑚 i 4 𝑐𝑚. Oblicz pole rombu.

wredulus_pospolitus: Sprawdź dane ... coś mi tu mocno się nie podoba i to mocno mi nie pasuje

Ika: No wlasnie tez mi cos nie pasuje bo wychodzi mi ze bok rombu ma dlugosc 16, a z tresci raczej ma 13

janek191: Tak jakby były dwa zadania w jednym

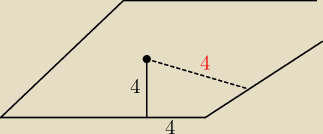
wredulus_pospolitus: Ika to nie wszystko ... druga sprawa skoro wysokość opuszczona przez środek okręgu dzieli bok na długości 9 i 4 ... to mamy taką sytuację Trochę mi tu 'śmierdzi' (tak wiem ... na rysunku nie jest to romb ... to nieistotne w tym momencie)

wredulus_pospolitus: Kuźwa ... bo to są dwa oddzielne zadania

Ika: No wlasnie na poczatku myslalam ze za mało danych zeby byly dwa oddzielne ale rzeczywiscie sie da obliczyc Już naprawde nie chcialo im sie tego rozdzielic na dwa czlowiek sie meczy

wredulus_pospolitus: 1) Dany jest romb ABCD. Wiedząc, że kąt ostry rombu ma miarę 30°, a promień okręgu wpisanego w romb jest równy 4, oblicz długości przekątnych tego rombu oraz jego obwód No i tutaj mamy: r = 4 −> d = 8 = h −> a = 16 P = ... Ob = ... 2) Wysokość rombu poprowadzona przez punkt przecięcia przekątnych dzieli bok rombu na odcinki mające długość 9 𝑐𝑚 i 4 𝑐𝑚. Oblicz pole rombu. oznaczamy e,f jako POŁOWY długości przekątnych. h jako połowę wysokości. e² + f² = 13² 9² + h² = e² 4² + h² = f² układ trzech równań

Ika: Dzięki bardzo!

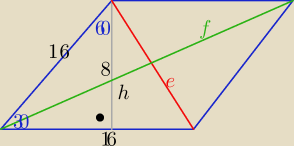
Eta: 1/ h=2r =8 to a= 16 z tw. cosinusów e²=16²+16²−2*16*16*cos30^o e²=16²(2−√3) e=16√2−√3 =========== f²+e²=4a² ⇒ f²=4a²−e² f²=16²(2+√3) f=16√2+√3 ==========

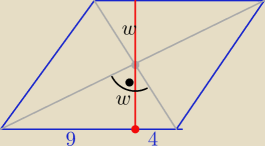
Eta: 2) w²=9*4 ⇒ w=6 to h=2w=12 i a=9+4=13 P=a*h=.............

Eta: Krótko: 1/ e=4r√2−√3 i f=4r√2+√3 ========================== gdy dane są : r−− dł. promienia okręgu wpisanego w romb o kącie ostrym 30^o