Sterometria - graniastosłup prawidłowy Kaz: Podstawą prostopadłościanu ABCDA₁B₁C₁D₁ jest kwadrat ABCD,a odcinki AA₁,BB₁,CC₁,DD₁ są krawędziami bocznymi. Oblicz odległość wierzchołka B1 od płaszczyzny ACD₁, wiedząc, że AB=a i AA₁=b.

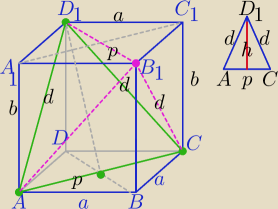
Mila: |AC|=p=a√2 d− przekątna ściany bocznej d=√a²+b² 1) Szukana odległość to wysokość (H) ostrosłupa ACD1B1 opuszczona na podstawę ACD1 z wierzchołka B₁ 2) obliczamy objętość tego ostrosłupa na dwa sposoby: V_g=a²*b Odcięto 4 naroża, które są też ostrosłupami, został czworościan ACD1B1.

	1		1		1
VABCB1=		*		*a*a*b=		a2b − objętość jednego naroża
	3		2		6

	1		1
VACD1B1=a2b−4*		a2b=		a2*b
	6		3

================================== W ΔACD₁:

	1		a√a2+2b2
h2=d2−(		p)2⇔h=
	2		√2

	1		1		1		a√a2+2b2
VACD1B1=		*PACD1*H=		*		*a√2*		*H=
	3		3		2		√2

	1		a√a2+2b2
=		*		*H
	3		2

======================== 3) Porównanie objętości:

1		a√a2+2b2		1
	*		*H=		a2*b
3		2		3

Stąd

	2ab
H=
	√a2+2b2

====================