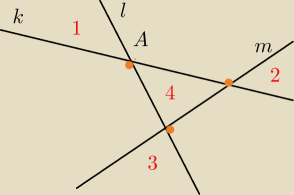
Trzy proste 6latek: Na plaszczyznie dane sa 3 rozne proste Znajdz na tej plaszczyznie wszystkie punkty z ktorych kazdy jest rowno oddalony od danych prostych Rozwaz rozne przypadki Przypadek nr 1 Trzy proste przecinaja sie w 3 punktach Beda to srodki czterech okregow stycznych do tych prostych Teraz pytanie Czyli musze wpisac okregi do obszarow oznaczonych numerami 1,2,3,4 Wpisac okrag w obszar nr 4 nie ma problemu Srodek okregu wpisanego w obszar nr 4 bedzie rowno odlegly od prostelj klm Jest problem z obszarem 1, 2 3 Wezmy dla przykladu nr 1 Jesli wyznacze dwusieczna kąta A to wtedy wszystkie srodki okregow wpisanych w ten kąt beda lezec na jego dwusiecznej (czyli te srodki tych okregow beda rowno odlegle od prostej k i l ) Tak ?

wredulus_pospolitus: 1) Jeżeli wszystkie proste się przecinają to wyznaczasz dwusieczne kąta A i kąta B (powiedzmy, że to ten przy 3) ich przecięcie daje Ci szukany punkt. Zauważ, że dokładnie w ten sposób (wyznaczając dwusieczne) wyznacza się środek okręgu wpisanego w trójkąt

wredulus_pospolitus: Bo chodzi o równą odległość do WSZYSTKICH trzech prostych, tak ?!

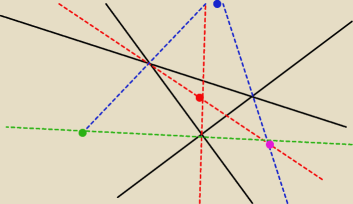
wredulus_pospolitus: więc (1) masz: jeden punkt drugi punkt (poza wykresem) trzeci punkt czwarty punkt (zauważ, że zielona, niebieska i czerwona dwusieczna musi się przeciąć przetnie się tam w jednym punkcie)

wredulus_pospolitus: tak samo jak ta 'pionowa' czerwona z niebieskimi ... i jak dwusieczna która byśmy poprowadzili z 'prawego przecięcia' musiałaby się przeciąć z dwoma czerwonymi oraz z niebieską i zieloną

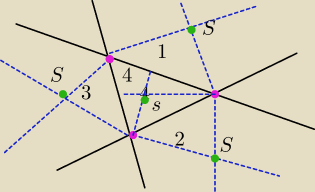
6latek: Rysunek zrobilem sam Podpowiedz jest taka jak napisalem jesli proste przecinaj sie w 3 punktach to szukanymi punktami beda srodki 4 okregow stycznych do tych prostych 18 : 51 chyba tak Wredulus a moze to trzeba w te obszary wpisac ? Te niebieskie przerywane to dwusieczne S− srodki okregow wpisanych

6latek: Zrobie dokladny rysunek i sprawdze .

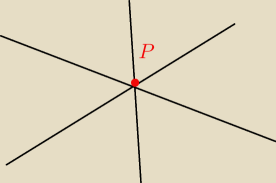
6latek: Przypadek nr 2 Proste przecinaja sie w jednym punkcie Tutaj ten punkt P bedzie rozwiazaniem

wredulus_pospolitus: oki

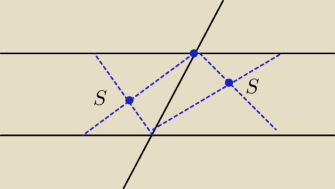
6latek: Przypadek nr 3 Mam dwie proste rownolegle i sa one przeciete trzecia prosta Beda to srodki okregow stycznych do danych prostych (niebieskie to dwusieczne

6latek: Bedzie przypadek nr 4 Wszystkie proste sa rownolegle Tutaj nie znajdzie sie takich punktow

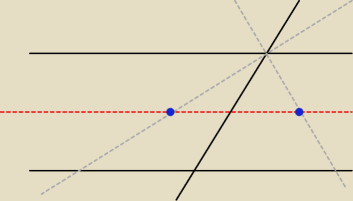
wredulus_pospolitus: 3)

wredulus_pospolitus: Zauważ, że u Ciebie 'wizualnie' punkty S nie leżą na prostej równoległej do dwóch prostych do siebie równoległych ... wiem że to szkic ... ale jakoś mnie to raziło w oczy

wredulus_pospolitus: Żeby nie było −−− ja także perfekcyjnie dwusiecznych nie wyznaczyłem (sprawdzałem rysując okrąg )

6latek: Wiesz w zeszycie zrobilem dobrze Cyrklem i linijka

6latek: Bylo jeszce zadanie na symetralna ale juz go zrobilem Mam nadzieje ze juz takich wiecej zadan w tym dziale nie bedzie