Stereometria Asd: W graniastosłupie prawidłowym sześciokątnym poprowadzono płaszczyznę, która przechodzi przez krawędź podstawy oraz przez środek symetrii graniastosłupa. Płaszczyzna ta wyznacza przekrój o polu równym 48√2 . Stosunek wysokości graniastosłupa do długości krawędzi podstawy jest równy √5 . Oblicz objętość tego graniastosłupa. Dlaczego przekrojem jest tu szesciokat?Bylbym wdzieczny jakby ktos mi zobrazowal srodek symetrii tego graniastoslupa,bo chyba przez to,ze o nim wspomnieli przekroj wyglada tak a nie inaczej ?

Mila: https://www.zadania.info/d498/5913383

Asd: Tak widziałem to,ale sobie nie moge jakos wyobrazić,że płaszczyzna przechodząca przez tą krawędź podstawy przechodzi też przez ta odleglosc CD na rysunku tym na stronie

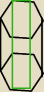
Asd: Bardziej mi sie takie cos wyobraza,mimo,ze inaczej by sie wtedy tresc zadania prezentowala

Mila: To spróbuj tak przeciąć ołówek, aby nie przeciąć brzegów , tylko w środek włożysz nóż? Prostokątem będzie przekrój prostopadły do podstaw.

Asd: Takie wytlumaczenie do mnie przemawia,nie pomyslalem Dziekuje

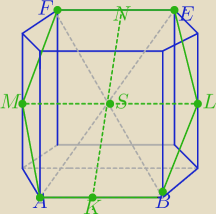
Mila: Przekrój ma przechodzić przez punkt S. E jest symetryczny do A względem S F jest symetryczny do B względem S L jest symetryczny do M względem S Tniemy ukośnie , aby przejść przez te punkty.