Boki trójkąta ABC zawarte są w prostych o równaniach 3x-y-9=0, 2x-1=0, x+y=3 Obl Tymon: Boki trójkąta ABC zawarte są w prostych o równaniach 3x−y−9=0, 2x−1=0, x+y=3 Oblicz pole koła opisanego na tym trójkącie.

6latek: Zrob chociaz raz sam rysunek do zadania i zastanow sie co mozna zrobic

Tymon: a jak wygląda wykres 2x−1=0?

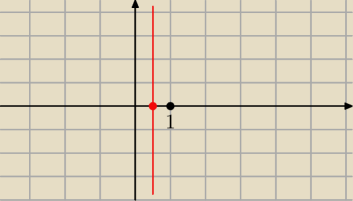
6latek: 2x=1

	1		1
x=		prosta rownolegla do osi OY przechodzaca przez x=
	2		2

Tymon: już obliczyłem punkty trójkąta A=(¹₂, −¹⁵₂) B=(3,0)C=(¹₂,⁵₂) ale nie wiem co dalej

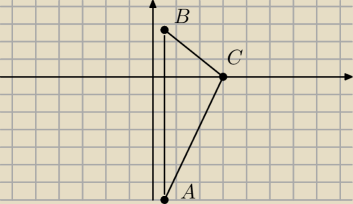
6latek: Te twoje wspolrzedne narysowalem Punkt A powinien byc nizej 1) Piszesz rownanie symetralnej np boku AB 2) Piszesz rownanie symetralnej boku np boku BC 3) obliczasz punkt przeciecia sie tych symetralnych 4) odlegosc np punktu C od punktu przeciecia sie symetralnych to promien kola (R) opisanego na tym trojkacie 5) pole kola =πR² jest to tylko jeden ze sposobow

Tymon: dzięki