Określ wzajemne położenie prostej l: -2x+4y-12=0 i okręgu x^2+y^2+12x-4y+31=0 Tymon: Określ wzajemne położenie prostej l: −2x+4y−12=0 i okręgu x²+y²+12x−4y+31=0 A. Prosta jest rozłączna z okręgiem, B. Prosta jest styczna do okręgu w punkcie P=(−5,¹₃). C.Prosta ma jeden punkt wspólny z okręgiem. D.Prosta ma dwa punkty wspólne z okręgiem. Prawidłowa odp to D.

wredulus_pospolitus: no i w czym problem ? −2x+4y − 12 = 0 2x = 4y − 12 x = 2y − 6 i podstawiasz do wzoru na okrąg. I gdy: a) brak rozwiązań −−− odp A b) jedno rozwiązanie −−− odp C (ewentualnie B) c) dwa rozwiązania −−− odp D Uwaga −−− jeżeli prawidłowa byłaby odpowiedź B to TAKŻE PRAWIDŁOWA byłaby C ... w efekcie, odpowiedź B z pewnością odpada

janek191: II sposób: x² + y² + 12 x − 4 y + 31 = 0 ( x + 6)² − 36 + ( y − 2)² − 4 + 31 = 0 ( x +6)² + ( y − 2)² = 3² S = ( − 6, 2) r = 3 oraz −2 x + 4 y − 12 = 0 / : (−2) x − 2 y + 6 = 0 Obliczam odległość tej prostej od środka okręgu S = ( − 6, 2)

	I 1*(−6) + (−2)*2 + 6 I		4
d =		=		< r
	√12 + (−2)2		√5

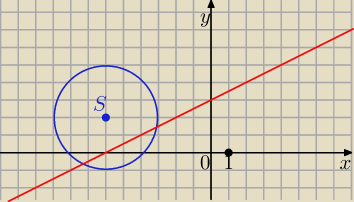
więc okrąg ma dwa punkty wspólne z daną prostą. Patrz też rysunek