Geometria analityczna Carlos: Dla jakich wwartości parametru k, k∊R, punkt przecięcia się prostych o równaniu 2x−3y−5k=0, x+3y+k−5=0 należy do prostokąta o wierzchołkach A=(1,1) B=(3,1),C=(3,6),D=(1,6)?

wredulus_pospolitus: Najprościej −− po prostu wyznacz punkt przecięcia się tych prostych (zależny od parametru k) i zobacz dla jakiego k, będzie należał do tego prostokąta

Carlos: a należeć to znaczy przecinać się przez odcinki tworzące prostokąt czy będące w środku również?

wredulus_pospolitus: Krawędzie (i wierzchołki) należą do figury

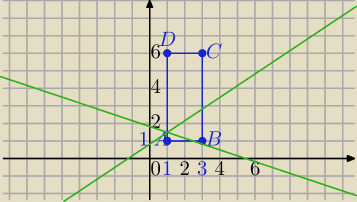
Mila: Punkt przecięcia prostych 2x−3y−5k=0, x+3y+k−5=0 należy do prostokąta o wierzchołkach: A=(1,1) B=(3,1),C=(3,6),D=(1,6) 1) Punkt przecięcia prostych: 2x−3y=5k x+3y=−k+5 3x=4k+5

	4k+5
x=
	3

	−7k+10
y=
	9

========== 2) 1≤x≤3 i 1≤y≤6⇔

	4k+5		−7k+10
1≤		≤3 i 1≤		≤6
	3		9

3≤4k+5≤9 /−5 i 9≤−7k+10≤ 54 /−10 −2≤4k≤4 /:4 i −1≤−7k≤44 /:(−7)

	1		1		44
−		≤k≤1 i		≥k≥−		⇔
	2		7		7

−1		1
	≤k≤
2		7

Sprawdzimy dla brzegowej wartości i wewnątrz.

	1
k=−
	2

proste:

	2		5		2		11
y=		x+		i y=−		x+		( zielone)
	3		6		3		6

	3
Punkt przecięcia: x=1, y=		∊do prostokąta
	2

posprawdzaj dalej