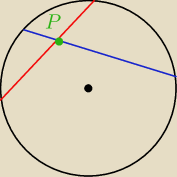
Okrag i cieciwy 6latek: Dwie cieciwy okregu o(O,r) przecinaja sie w punkcie P ≠O Uzasadnij ze punkt P nie moze byc wspolnym srodkiem obu cieciw

6latek: To zadanie jest tak troche dziko sformuowane Cieciwa jest prostopadla do promienia i promien dzieli ja na pol Wiec te cieciwy musialyby byc prostopadle zeby sie dzielily na pol Ale co ma do tego ze P≠O ?

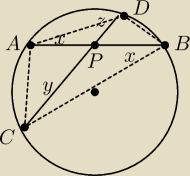
wredulus_pospolitus: Bez utraty ogólności możemy od razu założyć, że P jest w połowie jednej z cięciw. Dowód niewprost. zakładamy, że y = z wtedy: ΔAPC przystający do ΔBPD ΔAPD przystający do ΔBPC Tak więc: ∡CAD = ∡CBD Jako, że ACBD jest czworokątem wpisanym w okrąg to suma tych dwóch powyższych kątów wynosi 180^o Czyli są to kąty proste W takim razie ΔCAD jest prostokątny więc CD (przeciwprostokątna) przechodzi przez środek okręgu i ... chyba już sam dokończysz, prawda

wredulus_pospolitus: Cecha przystawania dla obu par kątów: BBK.

6latek: W zwiazku z tym punkt P =punktowi O czyli uzyskalismy sprzecznosc . Wniosek Jesli P≠O to P nie moze byc wspolnym srodkiem obu cieciw