Proste odcinek i punkt 6latek: Dane sa dwie rozne proste k i l ,punkt A i odcinek o dlugosci d Skonstruuj punkt P rowno oddalonych od prostych k i l zas od punktu A oddalony o d Pewnie tutaj trzeba bedzie rozpatrzyc dwa przypadki 1) proste sa rownolegle 2) proste nie sa rownolegle Gdzie ewentualnie moge znalezc opis tych konstrukcji?

b.: od punktu A oddalony o d −> czyli lezy na okręgu o środku w A i promieniu d rowno oddalonych od prostych k i l 1) proste sa rownolegle −> punkt leży na prostej równoległej do k i l leżącej ,,pośrodku'' nich (nietrudno skonstruować) 2) proste nie sa rownolegle −> punkt leży na jednej z dwóch dwusiecznych kątów wyznaczonych przez te proste jeśli okrąg ma punkt wspólny z prostą z 1) lub z którąś z prostych z 2), to taki punkt P istnieje, a jeśli nie, to nie

6latek: Dziekuje b Jutro to juz bede staral sie zrobic . Dobranoc

zys: do tego zadania był jakiś rysunek czy wszystko dowolne?

6latek: Nie bylo rysunku .

6latek: W tym zbiorze rysunki trzeba zrobic samemu

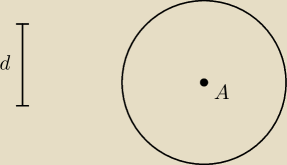
wredulus_pospolitus: 1) Bierzemy cyrkiel i odmierzamy długość 'd' 2) Robimy okrąg o promieniu d i środku w A 3) Jeżeli proste nie są równoległe − wyznaczamy punkt przecięcia się tych prostych 4) Następnie cyrklem wyznaczamy dwusieczną kąta (wiesz jak to zrobić? Jeżeli nie to pytaj) 5) Sprawdzamy gdzie dwusieczna przecina/jest styczną do okręgu 6) To jest miejsce punktu P 3*) Jeżeli proste są równoległe to wyznaczamy prostką m będąca równoległą do danych prostych, będącą równo odległą od tych prostych (w połowie odległości).

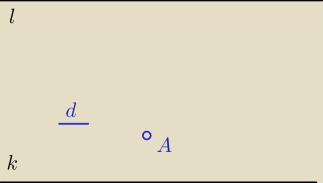
zys: ... dla prostych równoległych śą chyba ograniczenia (odległość prostych, połozenie punktu A i długość odcinka:

wredulus_pospolitus: zys −−− to samo ograniczenie masz gdy proste nie są równoległe gdy dwusieczna nie ma punktu wspólnego z okręgiem

zys: dlatego pytałem naszego Małolata czy zadanie ma jakiś rysunek

6latek: Przepraszam ze tak pozno sie odzywam Wiem jak wyznaczyc dwusieczna kąta za pomoca cyrkla (przypomniales mi ze nie kupilem temperowki

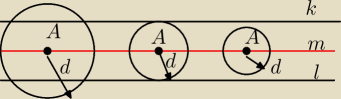
6latek: Dla prostych ki l jesli sa rownolegle to bedziemy mieli takie sytuacje w zaleznosci od odleglosci tych prostych i dlugosci odcinka d Punkt P jest czescia wspolna okregu i prostej m rowno oddalonej od prostych k i l Czyli punkt P bedzie lezal na prostej m

wredulus_pospolitus: tak ... punkt P leży na proste M i na okręgu o środku A i promieniu d. Przy czym punkt A nie musi leżeć na prostej m.

wredulus_pospolitus: Prosta m (czy w tym przypadku czy jako dwusieczna) załatwia nam sprawę 'równej odległości od prostych', okrąg zapewnia nam odległość od punktu A. Połączenie tych dwóch rzeczy daje nam wytyczne z zadania.

6latek: Witaj wredulus Za chwile wrzuce skan do 2 czesci zadania

6latek: <a href=https://zapodaj.net/82ce34908501e.jpg.html>001.jpg</a> Teraz nie wiem jak bo TY pisales ze ten okrag ma byc styczny do dwusiecznej a (b) pisze za ma lezec na dwusiecznej Mozesz pokazc ewentualnie jak to ma byc?

6latek: Zalezy mi na tym bo chce przejsc do nastepnego zadania , a jeszce musze isc narabac drzewa

Bleee: Nie pisałem że okrąg ma być styczny. Ma mieć punkt wspólny z wyznaczania prosta m, to samo napisał b.

6latek: Chodzi mi o proste nierownolegle

Bleee: No... I nadal... Pisałem o przecięcie lub styczności wyznaczanie prostej z okregiem... Czyli punkt wspólny o którym pisze b

Bleee: A co do rysunku − pamiętaj o drugiej dwusiecznej (prostopadlej do tej wyznaczonej)

6latek: tak pamietam