Wyznacz pochodną funkcji
Kam:
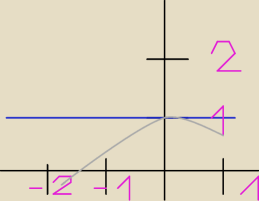
Na rysunku linią szarą zaznaczony jest wykres funkcji f a linią niebieską prosta styczna do
tego wykresu. Korzystając z danych na rysunku wyznacz F ' (0), a następnie wskaż prawidłowe
odpowiedzi.
a) F ' (0) = 1
b) F ' (0) jest prostą o równaniu y = x + 1
c) F ' (0) = 0
d) F ' (0) jest prostą o równaniu x = 1
Pomoże mi ktoś to rozwiązać? Za nic w świecie nie wiem jak się do tego zabrać. Wydaje mi się,
że muszę ustalić wzór funkcji f(x), a potem dzięki temu będę mógł dojść do odpowiedzi poprzez
podstawienie liczby 0 w miejsce x, ale nie wiem czy dobrze myślę.

10 mar 20:48
iteRacj@:
Funkcja f(x) ma w xo=0 maksimum. Jaka wartość ma dla xo=0 f.pochodna?
10 mar 20:55
Kam: 0?
10 mar 20:57
iteRacj@: Tak, a ustalanie wzoru funkcji f(x) nie jest potrzebne, nawet nie jest możliwe na podstawie
tego rysunku.
10 mar 21:00
Kam: Nie do końca rozumiem Twój sposób na rozwiązanie, mógłbyś wytłumaczyć?
10 mar 21:00
Kam: Czyli rozumiem, że odpowiedzią będzie c) F ' (0) = 0?
Co z innymi odpowiedziami? Tutaj może być wiele prawidłowych, ale nie musi.
10 mar 21:01
iteRacj@:
To jeszcze jedna informacja odczytana z wykresu. Styczna do wykresu f(x) w pkt xo=0 jest
równoległa od osi OX. Jaki jest jej współczynnik kierunkowy?
10 mar 21:04
Kam: Mówisz o stycznej koloru niebieskiego? Hmm… Jeżeli by rosła to dodatnia, jeżeli by spadała to
minusowy współczynnik kierunkowy, a ona stoi w miejscu. Ja bym tą styczną określił jako y=1
10 mar 21:07
iteRacj@: Dobrze podałeś jej równanie.
Jaki współczynnik kierunkowy ma prosta o równianiu y=1?
10 mar 21:09
Kam: 0, nie prawdaż?
10 mar 21:12
iteRacj@:
Tak, ten współczynnik kierunkowy ma wartość 0 i tak jest też wartość pochodenj dla xo=0.
Odp. c/ prawidłowa, a/ odpada
10 mar 21:13
Kam: b oraz d odpowiedz także odpada prawda?
10 mar 21:14
iteRacj@:
A wiesz dlaczego?
10 mar 21:14
Kam: Jeśli f(x) = sinex, to f ' (x) jest równe (dla każdego x, dla którego f ' (x) istnieje):
a) cosex
b) (cosx) * ex
c) (cosex) * (ex) '
d) (cosex) * ex
Jesteś w stanie to wytłumaczyć, jeżeli mogę Cię o to prosić?
10 mar 21:15
Kam: Hmm odpowiedz b oraz d nie podoba mi się, gdyż:
1) ta funkcja nie jest prostą, ale nie wiem czy dobrze myślę, ona jest parabolą.
10 mar 21:16
iteRacj@: f(x) = sin(e)x czy f(x) = sin(ex)?
10 mar 21:17
Kam: f(x) = sin * ex, czyli f(x) = sin(ex) wydaje mi się.
10 mar 21:19
iteRacj@:
Pochodna w punkcie 0 to liczba → b/, d/ odpada.
10 mar 21:19
Kam: Masz na myśli, że pochodną w punkcie f ' (0) = liczba, a nie wzór funkcji? Wybacz jeżeli zadaje
głupie pytania, ale nie jest ten dział dla mnie łatwy, a bardzo chce go zrozumieć.
10 mar 21:23
iteRacj@:
Zapis f(x) = sin * ex jest bez sensu.
Jeśli f(x) = sin(ex), to f'(x) = cos(ex) * ex
10 mar 21:24
Kam: W zadaniu mam dokładnie tak:
Jeśli f(x) = sin ex, to …….
Słownie: sinus (spacja) e podniesiona do potęgi x, to ….
10 mar 21:26
Kam: Ok ogarnąłem już o co Ci chodziło z tymi błędnymi odpowiedziami b oraz d. Skoro F ' (0) = 0 to
nie może być równe y = x+1 (odpowieedz b) lub y=1 (odpowiedz d)
10 mar 21:28
Kam: Czyli w tym drugim zadaniu odpowiedz d? Gdyż nie bardzo pokrywa się ona z Twoją odpowiedzią,
którą udzieliłeś. Mógłbyś to przy okazji wytłumaczyć chociaż trochę

?
10 mar 21:32
iteRacj@:
21:23 tak, pochodna w konkretnym punkcie to liczba.
Wzory z pkt b/, d/ mogłyby opisywać funkcję pochodną (czyli "przepis" na pochodne dla każdego
argumetu) jakiejś funkcji (nie tej z rysunku).
10 mar 21:34
Kam: Rozumiem, pierwsze zadanie wydaje mi się, że mniej więcej zrozumiałem.
10 mar 21:35
Kam: Jesteś w stanie wytłumaczyć drugie?
10 mar 21:37
iteRacj@:
podana funkcja F(x)=sin ex to funkcja złożona
pochodna f. złożonej
[f(g(x))]'=f'(g(x))*g(x)'
tutaj f. wewnętrzna to g(x)=ex, jej pochodna to g(x)'=1*ex
pochodna funkcji sin x to f.cos x (czyli ten sam argument)
f'(g(x))= cos(ex), g(x)'=1*ex
F'(x)= cos(ex) * ex
10 mar 21:48
Kam: Wszystko wygląda faktycznie na możliwe. Gdzieś już mi się "obił o uszy" ten wzór na fnkcję
złożoną. Masz chyba w 100% rację.
10 mar 21:51
Kam: Tylko problem w tym, że nie mam takiej odpowiedzi co Ty podałeś

10 mar 21:54
10 mar 21:55
Kam: moje odpowiedzi to
cos ex
(cosx) * ex
(cos ex) * (ex) '
(cos ex) * ex
10 mar 21:55
iteRacj@: to odpowiedź d/
10 mar 21:56
Kam:
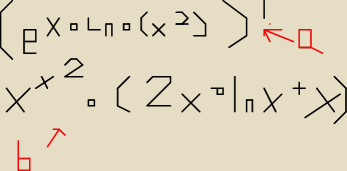
Ok, bardzo Ci dziękuje.
Pomożesz przy ostatnim? Wydaje się troszkę prostsze.
Jeśli f(x) = x
x2, to f ' (x) jest równa (dla wszystkich x, dla których f ' (x) istnieje):
c) 2 * x
x2 (x podniesione do x podniesione do 2)
d) x
2 * x
x2−1 (x podniesione do {x podniesione do 2}−1), czyli jedynke odejmij od x
2
10 mar 22:14
Kam: Jesteś w stanie pomóc z ostatnim?
10 mar 22:24
iteRacj@:
bardzo ładnie narysowane
odp. b/
10 mar 22:25
Kam: jedynie

?
Dziękuje

10 mar 22:28
iteRacj@: tylko b/
zapis a/ nie jest równoważny wyjściowemu wyrażeniu xx2
10 mar 22:36
Kam: a odpowiedz c) oraz d)?
10 mar 22:39
iteRacj@:
Czy poprawną odpowiedź b/ da się przekształcić do postaci c/ lub d/?
Nie, więc nie są to odp. prawidłowe.
10 mar 22:42
Kam: Ok, przeanalizuje. Moment.
10 mar 22:44
Kam: Masz rację, jedynie odpowiedz D jest odpowiedzią poprawną


Przeserdecznie Ci dziękuje. Nie wiem jak Ci się odwdzięczyć

10 mar 22:47
iteRacj@:
Ucz dalej innych matematyki : )
Albo czegoś innego, co lubisz, niech też to polubią.
10 mar 22:54
Kam: Piękne słowa jak i sposób odwdzięczenia się, zapamiętam to sobie

11 mar 20:41
 Na rysunku linią szarą zaznaczony jest wykres funkcji f a linią niebieską prosta styczna do
tego wykresu. Korzystając z danych na rysunku wyznacz F ' (0), a następnie wskaż prawidłowe
odpowiedzi.
a) F ' (0) = 1
b) F ' (0) jest prostą o równaniu y = x + 1
c) F ' (0) = 0
d) F ' (0) jest prostą o równaniu x = 1
Pomoże mi ktoś to rozwiązać? Za nic w świecie nie wiem jak się do tego zabrać. Wydaje mi się,
że muszę ustalić wzór funkcji f(x), a potem dzięki temu będę mógł dojść do odpowiedzi poprzez
podstawienie liczby 0 w miejsce x, ale nie wiem czy dobrze myślę.
Na rysunku linią szarą zaznaczony jest wykres funkcji f a linią niebieską prosta styczna do
tego wykresu. Korzystając z danych na rysunku wyznacz F ' (0), a następnie wskaż prawidłowe
odpowiedzi.
a) F ' (0) = 1
b) F ' (0) jest prostą o równaniu y = x + 1
c) F ' (0) = 0
d) F ' (0) jest prostą o równaniu x = 1
Pomoże mi ktoś to rozwiązać? Za nic w świecie nie wiem jak się do tego zabrać. Wydaje mi się,
że muszę ustalić wzór funkcji f(x), a potem dzięki temu będę mógł dojść do odpowiedzi poprzez
podstawienie liczby 0 w miejsce x, ale nie wiem czy dobrze myślę. 
 ?
?

 https://www.wolframalpha.com/input/?i=%5Bsin(e%5Ex)%5D%27
https://www.wolframalpha.com/input/?i=%5Bsin(e%5Ex)%5D%27
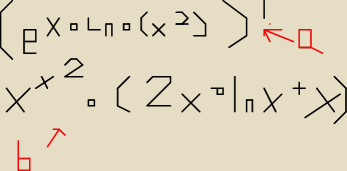 Ok, bardzo Ci dziękuje.
Pomożesz przy ostatnim? Wydaje się troszkę prostsze.
Jeśli f(x) = xx2, to f ' (x) jest równa (dla wszystkich x, dla których f ' (x) istnieje):
c) 2 * xx2 (x podniesione do x podniesione do 2)
d) x2 * xx2−1 (x podniesione do {x podniesione do 2}−1), czyli jedynke odejmij od x2
Ok, bardzo Ci dziękuje.
Pomożesz przy ostatnim? Wydaje się troszkę prostsze.
Jeśli f(x) = xx2, to f ' (x) jest równa (dla wszystkich x, dla których f ' (x) istnieje):
c) 2 * xx2 (x podniesione do x podniesione do 2)
d) x2 * xx2−1 (x podniesione do {x podniesione do 2}−1), czyli jedynke odejmij od x2
 ?
Dziękuje
?
Dziękuje 

 Przeserdecznie Ci dziękuje. Nie wiem jak Ci się odwdzięczyć
Przeserdecznie Ci dziękuje. Nie wiem jak Ci się odwdzięczyć 
