wykres funkcji grzegorzz: mam zadanko,

	2x
Narysuj wykres funkcji f(x) = I		I. na podstawie wykresu określ liczbę
	x − 3

	2x
rozwiązań równania I		i = m w zależności od parametru m. Jak nawet narysować
	x − 3

ten wykres?

PW:

2x		2(x−3)+6		6
	=		= 2 +		,
x−3		x−3		x−3

a to umiemy narysować, o funkcji homograficznej mówiło sie w szkole.

Eta:

	6
1/ narysuj wykres f1=
	x

przesuń go o wektor [3,2]

	6
f2=
	x−3

odbij tę część wykresu spod osi OX nad ośOX

	6
otrzymasz f(x)= |		+2| , x≠3
	x−3

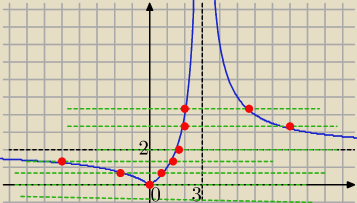
tniemy wykres prostymi y=m 0 rozwiązań dla m<0 1 rozwiązanie dla m=2 v m=0 2 rozwiązania dla m∊(0,2) U ((2,∞)

Mila:

	2x		2x−6+6		2*(x−3)+6
g(x)=		=		=
	x−3		x−3		x−3

	6
g(x)=2+
	x−3

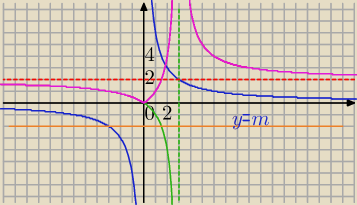
1)

	6
rysujesz wykres : y=
	x

2) Przesunięcie o wektor [3,2]⇒otrzymujesz wykres g(x) 3) |g(x)| ⇒otrzymujesz wykres f(x)

	2x
4) |		|=m
	x−3

m<0 brak rozwiązań m=0 − jedno rozwiązanie m∊(0,2)− dwa rozwiązania spróbuj dalej sam, przesuwasz prostą y=m do góry

grzegorzz: Przerobię podobne zadania i mam nadzieje ,że zrozumiem Dziękuje wszystkim za zaangażowanie

Eta: dla m=2 też 1 rozwiązanie

Eta: 2 rozwiązania jeszcze dla m∊(2,∞)