Dla jakich wartości parametru a a∊R prosta o równaniu y=ax-4 jest styczna do okr Tymon: Dla jakich wartości parametru a a∊R prosta o równaniu y=ax−4 jest styczna do okręgu o równaniu (x−4)²+(y+2)²=4?

Jerzy: Np,tak: podstaw y do równania okręgu i warunek 1 rozwiązanie.

wredulus_pospolitus: innymi słowy ...kiedy równanie: (x−4)² + ((ax−4)+2)² = 4 ma JEDNO ROZWIĄZANIE

janek191: S = ( 4, − 2) r = 2 Odległość tej prostej od S musi być równa 2.

Tymon: czyli wtedy kiedy delta równa się zero tak?

wredulus_pospolitus: albo gdy a² + 1 = 0 (co jest nierealne ... no ale nadmienić trza)

Tymon: w sumie to po rozpisaniu tego równania nie wiem co trzeba zrobić dalej: x²−8x+16+(ax−4)²+4(ax−4)+4=4 x²−8x+16+(ax)²−8ax+16+4ax−16+4=4 x²−8x+16+(ax)²−4ax=0

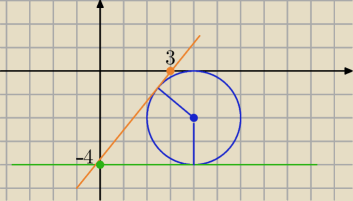
Eta: 1) a= 0 bo y=−4 −− styczna

	4		4
2/ a=		bo y=		x−4 ma miejsce zerowe xo= 3
	3		3

S(4,−2) r=2 s: ax−y−4=0

	|4a+2−4|
d=		=2 ⇒ |2a−1|=√a2+1 ^2
	√a2+1

(2a−1)²=a²+1 3a²−4a=0 a(3a−4)=0

	4
a=0 v a=
	3

================ co zgadza się z rys.

Tymon: dziękuje teraz wszystko jasne

Eta: