Podobieństwo Domestosus: Przez punkt K, leżący na boku AB trójkąta ABCpoprowadzono prostą równoległą do boku ACi przecinającą bok BCw punkcie Loraz prostą równoległą do boku BCi przecinającą bok ACw punkcie M. Pola trójkątów KBLi KMAsą równe odpowiednio 9 i 49. Oblicz pole trójkąta ABC

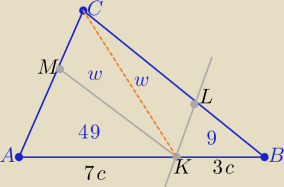
Eta: 1/ rysunek 2/ Z cechy (kkk) ΔAKM ∼ ΔABC i ΔBKL ∼ΔABC ⇒ ΔAKM ∼ΔBKL

	49		7
w skali k >0 ;		=k2 ⇒ k=
	9		3

czworokąt KLCM jest równoległobokiem wię jego pole P=2w P(ABC)=49+9+2w ⇒ P(ABC(=58+2w trójkąty AKC i BKC mają wspólną wysokość opuszczoną na podstawę AB

	w+49		7
to:		=		⇒ 2w=42
	w+9		3

P(ABC)=100 ===========

Eta: Domestosusa zamurowało?