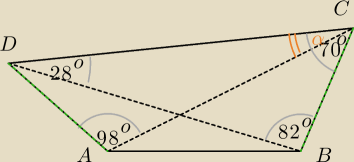
Jagielloński Turniej Matematyczny II, Etap IIIA zakończony tydzień temu iteRacj@: W czworokącie ABCD mamy |∢DAC|=98^o, |∢DBC|=82^o, |∢BCD|=70^o oraz |BC|=|AD|. Znaleźć miarę kąta ACD. Rysując rysunek do tego zadania, zobaczyłam zręczne rozwiązane, którego wcześniej nie widziałam (pozytywna energia tego forum), ale zadanie zostawiam, może się komuś przyda do nauki.

Adamm: β = |kąt ADC| α:β = 28:70 ⇒ β = 70α/28 98^o+β+α = 180^o α = (164/7)^o

Adamm: Nie do końca, ale można poprawić. sin(α)/sin(98^o) = sin(28^o)/sin(82^o) sin(α) = sin(28^o) α = 28^o, bo α musi być ostry

Adamm: Ciekawi mnie rozwiązanie bez trygonometrii.

iteRacj@: Nie podam, też skorzystałam z tw. sinusów.