Kula w stożku, klasyka Ateusz: Tworząca stożka o objętości V jest nachylona do płaszczyzny podstawy pod kątem x. Oblicz objętość kupi wpisanej w ten stożek. Poprzekształcałem boki trójkąta równoramiennego będącego przekrojem osiowym stożka, tak, aby

	3V
objętość V mieć zależną od jednej zmiennej (wybrałem r) wyszło mi r=3√
	pi*tgx

Obliczyłem pole trójkąta, (jego wysokość jak i bok uzależnione miałem od tej samej jednej zmiennej r) P=r²tgx Następnie skorzystałem ze wzoru na pole trójkąta P=p*R (R to promień kuli wpisanej w stożek) Przyrównałem wcześniej obliczone pole, do p*R. Po czasochłonnych przekształceniach wyszło mi,

	rsinx
że R=
	1+cosx

	12V*sin2x
Zatem objętość kuli wpisanej w stożek wyszła mi równa		=
	cosx(3+3cosx)

	4V*tgx*sinx
	1+cosx

Czy sposób rozwiązywania jak i rozwiązanie są poprawne?

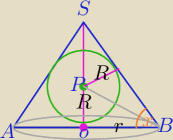
Mila: Pomysł dobry, ale mogłeś skrócić tę męczarnie rachunkową.

	3V
1) r3=
	πtgx

============ 2)Środek okręgu wpisanego w Δ leży na przecięciu dwusiecznych kątów Δ. W ΔBOP:

	x		R
tg		=
	2		r

	x
R=r*tg
	2

3)

	4π		4π		x
Vk=		R3=		*r3*tg3		=
	3		3		2

	4π		3V		x
=		*		*tg3
	3		πtgx		2

	4V		x
Vk=		*tg3		i tak bym zostawiła.
	tgx		2

Ateusz: @Mila dzięki, zaraz spróbuję sposobem z dwusiecznymi i zobaczę co wyjdzie. Ale czy ten mój wynik jest tożsamy z twoim?

Mila: Po co próbować, masz napisane. Powinien być, bo R jest.

	x		sinx
tg		=
	2		1+cosx

Ateusz: @Mila Wolę zawsze wszystko zrobić samemu, a jak coś nie wyjdzie, albo stanę w miejscu bez dalszego pomysłu, to dopiero wtedy zaglądam po jakąś wskazówkę Dzięki za pomoc

Mila: Powodzenia