. sylwiaczek: przez punkt P(1,9) poprowadzono prosta o wspolczynniku kierunkowym ujemnym tak, ze suma dlugosci odcinkow ktore ta prosta odciela na osiach ukladu wspolrzednych jest najmniejsza. Wyznacz rownanie tej prostej

jc: Załóżmy, że prosta przechodzi przez (a,b). Odcinki odcięte na osiach: p, q. a/p + b/q=1 Nierówność Schwarza dla wektorów u=(√a/p, √b/q), v=(√p, √q) (u*v)² ≤ u² v² (√a + √b)² ≤ p+q Najmniejszą wartość uzyskujemy, jeśli u||v. p=(√a+√b)√a q=(√a+√b)√b Równanie prostej x/p+y/q=1

jc: Nie wiem, jak to zapisać w Twojej notacji. q(10), p(90), prosta k(1/10,1/90,1).

ICSP: y = ax + b 9 = a + b ⇒ b = 9 − a y = ax + 9 − a − "pęk prostych" przechodzących przez punkt (1 ; 9 ) przecięcie z osią odciętych:

	a − 9
(		; 0)
	a

przecięcie z osią rzędnych : (0 ; 9 − a) Suma odcinków licząc od (0;0)

	a − 9
f(a) =		+ 9 − a
	a

minimum dla a = − 3 Swoją drogą chyba, źle zrozumiałem polecenie. Mamy prostą która przecina oś odciętych i rzędnych w dokładnie jednym punkcie. Czyli każdy z odcinków na które ta prosta podzieliła osie "ma długość ∞".

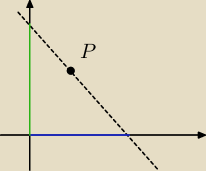
iteRacj@: W popularnym zbiorze znanego maturzystom autora to mają byc odcinki wyznaczone przez te punkty współne i początek układu współrzędnych.

iteRacj@: *wspólne prostej z osiami

jc: (a,b)=(1,9) p=4 q=13 prosta x/4+y/12=1 lub inaczej 3x+y=12