Trójkąt Paweł: Witam, mam takie zadanie. W trójkąt równoramienny mam wpisany okrąg, którego środek dzieli wysokość, poprowadzoną na podstawę w odpowiednim stosunku liczonym od wierzchołka, powiedzmy, że ten stosunek to x:y. Mam dane tylko tyle. Jak z tymi danymi obliczyć promień okręgu opisanego na tym trójkącie? Proszę o jakieś wskazówki.

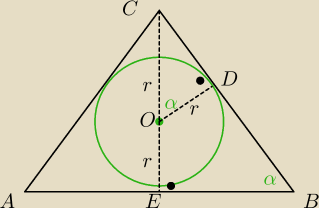
iteRacj@: |CE|=h, |CO|=h*x=h−r, |EO|=h*y=r R − promień promień okręgu opisanego na Δ z tw. sinusów

h
	=2R
sin α

	hy
sin α=		// wyliczam z ΔCOD
	hx

iteRacj@: Żeby obliczyć, ile centymetrów ma promień, musisz znać długość któregoś z boków albo np. wysokość trójkąta. Ja przyjęłam za daną wysokość.

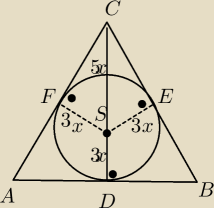
Paweł: Miałem dany ten stosunek 5:3. Doszedłem do tego, że 3x to będzie promień okręgu wpisanego. Obliczyłem lCEl wyszło mi 4x z Pitagorasa. Później Z podobieństwa trójkątów wyszło mi, że lEBl − 6x i lDBl= 6x. Później z tw. sinusów i wyszło mi, że promień to 5x. Ale nie mam nic danego prócz tego stosunku i nie wiem, czy gdzieś się pomyliłem i dlatego nadal wszystko mam uzależnione od x czy tak już to zostawić

iteRacj@: Istnieje nieskończenie wiele trójkątów równoramiennych, w których taka proporcja wynosi 5:3. Są to trójkąty podobne. Jeśli wynik ma dotyczyć konkretnego trójkąta, to musisz znać x. U Ciebie 19:10 nie da się więcej ustalic niż to, że szukany promień ma 5x.

	y
Teraz zauważyłam u siebie błąd,		=cos α .
	x

Paweł : Dzięki, chciałem porównać wyniki i chyba tylko tyle mogę zrobić. Bardzo dziękuję. 😉