Jednokładność matura11: Dany jest kwadrat ABCD O wierzchołkach A=(−8,3)B=(−5,2)C=(−4,5)D=(−7,6). Obraz jednego z tych wierzchołków w jednokladnosci o środku w punkcie A i skali ujemnej leży na prostej l o rówwnaniu x−2y−6=0. Wyznacz współrzędne wierzchołków obrazu kwadratu ABCD w tej jednokladnosci. Jest rozwiązane na forum, ale nie rozumiem tamtej metody

iteRacj@: To podaj link do tamtego rozwiązania i napisz, co jest niejasne.

Mila: Czego tam nie rozumiesz?

matura11: Dlaczego od razu liczmy długość AD i wszystko dla punktu D?

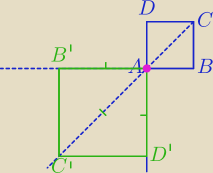
Mila: Przykład przekształcenia dla skali ujemnej. Jednokładność o skali k=−2 Czy z tym masz problem?

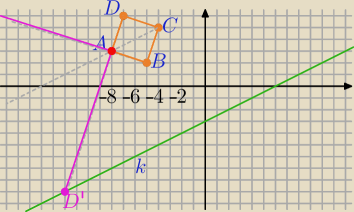
Mila: A=(−8,3), B=(−5,2), C=(−4,5), D=(−7,6). x−2y−6=0

	1
k: y=		x−3
	2

1) Mamy obliczyć skalę jednokładności, to musimy mieć punkt przecięcia jednej z trzech półprostych: CA^→, BA^→, DA^→ możesz pisać równania tych trzech prostych, ale tylko DA przetnie prostą k. 2) prosta DA y=ax+b 3=−8a+b 6=−7a+b −−−−−−−−−−−odejmuje stronami −a=−3, a=3 , y=3x+b, 3=3*(−8)+b, b=27 y=3x+27 3) Punkt przecięcia:

	1
3x+27=		x−3
	2

	1
x=−12, y=		*(−12)+3=−9
	2

D'=(−12,−9) 4) Skala jednokładności Poradzisz sobie?

matura11: Tak! dzięki, zrobione!

Mila: