full stereo dolby hd Ateusz: Dany jest stożek o wysokości długości h i promieniu podstawy długości r. Oblicz długość krawędzi sześcianu wpisanego w stożek w ten sposób, że dolna podstawa sześcianu zawiera się w podstawie stożka, a wierzchołki górnej podstawy sześcianu należą do powierzchni bocznej stożka. probowalem podobienstwa trojkatow ale nie wychodzilo czy gorna podstawa szescianu stworzy wraz z wierzcholkiem stozka drugi stozek o podstawie, w ktora wpisany jest kwadrat (gorna podstawa szescianu)?

Ateusz: ta wtedy stosunki z podobienstwa obu przekrojow beda sie zgadzac, bo wczesniej za podstawy podstawialem 1/2a a biorąc pod uwage tezę, ktora sam sobie potwierdzilem powinienem podstawic 1/2a√2 ale jeszcze prosze o potwierdzenie

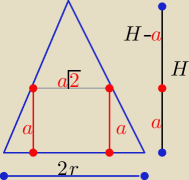
Eta: Tak wygląda przekrój z podobieństwa trójkątów

a√2		H−a		2rH
	=		⇒ ........ a=
2r		H		H√2+2r

Eta: https://www.geogebra.org/m/s2uRPiuj