 Jeden ze sposobów
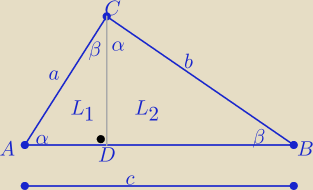
Z podobieństwa trójkątów
ΔADC∼ ΔABC i ΔDBC ∼ ΔABC
Jeden ze sposobów
Z podobieństwa trójkątów
ΔADC∼ ΔABC i ΔDBC ∼ ΔABC
| L1 | a | L2 | b | b | ||||||
(*) | = | i (**) | = | to L2=L1* | ||||||
| L | c | L | c | a |
| 5 | 4 | |||
(*) c= | a to b= | a | ||
| 3 | 3 |
| 5 | 10 | |||
L=a+b+c= .... =4a=10 ⇒ a= | to b= | |||
| 2 | 3 |
| 10 | 2 | |||
L2=6* | * | |||
| 3 | 5 |
| 10 | 25 | 5 | ||||
b= | , c= | , a= | ||||
| 3 | 6 | 2 |
| ab | ||
h= | =2 | |
| c |