Trójkąt w układzie współrzędnych john: Witam może mi ktoś powiedzieć gdzie mam błąd: Boki AB i CA trójkąta ABC są zawarte w prostych y + 12 = 7x i 2y + x = 6 , a jego dwa wierzchołki mają współrzędne B = (1 ,− 5 ) i C = (10,− 2) . Oblicz pole tego trójkąta. Liczę A z układu: y = 7x − 12

	1
y = −		x + 3
	2

	1
7x − 12 = −		+ 3
	2

12
	x = 15
2

x = 2 y = 2 A = (2, 2) Teraz liczę długość podstawy |BC| którą wykorzystam do wyliczenia pola: |BC| = √(1 − 10)² + (−5 + 2)² = √90 = 3√10 Liczę wektor BC: BC = C − B = (10 − 1, −2 + 5) = (9, 3) D = B + połowa wektora BC

	BC		9		3		11		7
D = B +		= (1, −5) + (		,		) = (		, −		)
	2		2		2		2		2

I wysokość:

	11		7		√170
|AD| = √(2 −		)2 + (2 +		)2 =
	2		2		2

Pole:

	3√10		√170		3√1700
P =		*		=
	2		2		4

Ale powinno wyjsc: 30

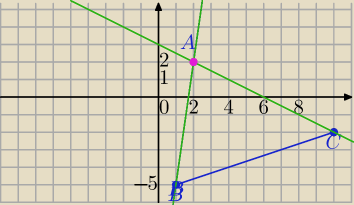
Mila: B = (1 ,− 5 ) i C = (10,− 2) y + 12 = 7x i 2y + x = 6 y=7x−12

	1
y=−		x+3
	2

A=(2,2) BC^→=[9,3] BA^→=[1,7]

	1
PΔ=		*|W|
	2

W=9*7−3*1=60

	1
PΔ=		*60=30
	2

dero2005: A(2,2) B(1,−5) C(10,−2) S = ¹₂(x_A−x_B)(y_C−y_A)−(y_B−y_A)(x_C−x_A) = 30

Jolanta:

	1		1
prosta na ktorej lezą wierzcholki Bi C ma wzóry=		x−5		.policzyłam wysokość czyli
	3		3

odległość punktu A od tej prostej i wyszła mi 2√10. chyba liczyłeś,że wysokość lezy w połowie odcinka BC i to było błędne

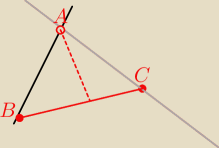
szymon: Pakujesz sie w niepotrzebne trudności Łatwiej będzie policzyć długość odcibka BC a później wysokość (odległość A od prostej BC)

john: Dzięki Jolanta, nie zauważyłem że bezpodstawnie założyłem że wysokość przecina BC w połowie, jak już chciałem tak kombinować z wektorami to powinienem skorzystać z tego że iloczyn skalarny prostopadłych ma wynosić 0, ale faktycznie tutaj chyba lepiej użyć prostych jak mówi Szymon, albo zrobić tak jak Mila, lub jeszcze szybciej tak jak dero2005. Nie wiedziałem wcześniej o tym wzorze.