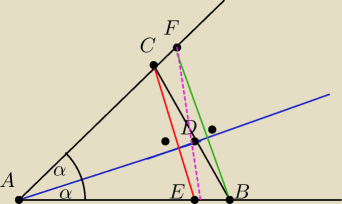
dwusieczna i trojkat 6latek: Dwusieczna kąta A w trojkacie ABC przecina bok BC w punkcie D Z wierzcholka B i C poprowadzono proste prostopadle do AD przecinajace proste AC i AB odpowiednio w punktach E i F Wykaz ze ΔABC jest przystajacy do ΔAEF oraz ze punkty EDF sa wspolliniowe

6latek: Chyba moge skorzystac z faktu ze jesli dwie proste sa prostopadle do trzeciej prostej to sa one do siebie rownolegle Teraz nalezy wykazac ze AB= CF I teraz skorzystac z faktu o prostych rownoleglych przecietych sieczna ?

iteRacj@: Punkt wspólny dwusiecznej i odcinka CE oznaczam G, punkt wspólny dwusiecznej i odcinka BF oznaczam H. ΔACG i ΔAEG są przystające (kbk) ⇒ |AC|=|AE| ΔAFH i ΔABH są przystające (kbk) ⇒ |AF|=|AB| I to są już wystarczające dane, żeby wykazać przystawanie trójkątów ΔABC i ΔAEF.

6latek: Dzien dobry Dzieki za odzew . Mam wskazowke do zdania . najpierw wykaz ze czworokat BECF jest trapezem rownoramiennym

6latek: I teraz z przystawania tych trojkatow mam ze EB=CF a to oznacza ze czworokat BECF jest trapezem rownoramiennym Stad wynika wspolliniowosc punktow EDF

ite: Wydaje mi się, że samo napisanie "stąd wynika współliniowość" to mało. Może lepiej jest dodać wyjaśnienie: Odcinek CB jest przekątną tego trapezu, D środkiem tej przekątnej. Odcinek FE to druga przekątna, a skoro przekątne trapezu równoramiennego przecinają się w połowie, to D jest też środkiem drugiej przekątnej. Czyli pkt D należy do odcinka FE, więc punkty F,D,E są współliniowe.

6latek: dziekuje ite