równanie wielomianowe
Kati20: rozwiąż równanie
−0,125x3+1,5x2−4,5x+8=0
7 mar 11:58
6latek: | | 1 | | 3 | | 9 | |
− |
| x3+ |
| x2− |
| x+8=0 (*8 |
| | 8 | | 2 | | 2 | |
−x
3+12x
2−36x+64=0
7 mar 12:04
ABC:
Kati dobrze przepisane? bo nie ma ładnych pierwiastków

7 mar 12:27
6latek: Witaj

7 mar 12:28
zys:
... jak to nie ma

Równanie 3−stopnia musi mieć przynajmniej jeden pierwiastek
7 mar 12:47
ABC:
cześć 6latek

zys no to rozwiązuj, ja popatrzę czy jesteś tak dobry jak Mariusz

7 mar 12:55
zys:
... nic Ci nie muszę udowadniać. Chcesz to licz ... ma pierwiastek w przedziale (8, 9)
7 mar 12:57
PW: Panowie, szkoda życia na takie rachunki. Poczekajmy co powie Kati20 − czy na pewno dobrze
przepisane, do której klasy chodzi i tak dalej.
7 mar 13:55
PW:
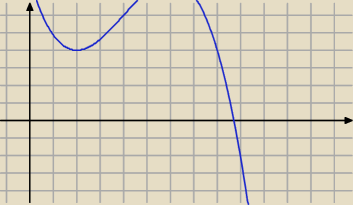
7 mar 13:58
Kati20: Na pewno dobrze przepisane i racja pierwiastek jest jeden 8.701 ale problem mam do tego dojsc
7 mar 16:50
PW: A na jakim poziomie rozpatrujesz to zadanie? Jest to szukanie przybliżeń metodami numerycznymi?
7 mar 17:41
Kati20: PW dziekuje za wskazówkę juz wiem jak obliczyć

7 mar 18:08
Mariusz:
−x
3+12x
2−36x+64=0
x
3−12x
2+36x−64=0
Najpierw usuwasz wyraz z x
2
Tutaj przydatne będą wzory skróconego mnożenia
i opcjonalnie schemat Hornera
x
3−12x
2+36x−64=0
(x−4)
3=x
3−12x
2+48x−64
(x−4)
3−12(x−4)=x
3−12x
2+36x−64+48
(x−4)
3−12(x−4)−48=x
3−12x
2+36x−64
y=x−4
y
3−12y−48=0
Zakładasz że pierwiastek jest w postaci sumy dwóch składników
y = u + v
Wstawiasz y=u+v do równania , korzystasz ze wzoru skróconego mnożenia
a następnie grupujesz wyrazy w wyrażeniu algebraicznym
(u+v)
3−12(u+v)−48 = 0
u
3+3u
2v+3uv
2+v
3−12(u+v)−48 = 0
u
3+v
3−48+3(u+v)(uv−4)=0
Zapisujesz powyższe równanie w postaci układu równań
u
3+v
3−48=0
3(u+v)(uv−4)=0
Zapisaliśmy układ równań w ten sposób bo jeden ze składników jest iloczynem
Zauważ że wcześniej przyjęliśmy że u+v=y więc
na ogół nie możemy przyrównać tego czynnika do zera
u
3+v
3−48=0
uv−4=0
u
3+v
3=48
uv=4
Powyższy układ równań łatwo przekształcić we wzory Vieta dla trójmianu kwadratowego
o pierwiastkach u
3 oraz v
3
u
3+v
3=48
uv=4
u
3+v
3=48
u
3v
3=64
t
2−48t+64=0
(t−24)
2−576+64=0
(t−24)
2−2*256=0
(t−24−16
√2)(t−24+16
√2)=0
(t−(24+16
√2))(t−(24−16
√2))=0
y=
3√24+16√2+
3√24−16√2
x−4=
3√24+16√2+
3√24−16√2
x=
3√24+16√2+
3√24−16√2+4
Jak widzisz jeden przykład nie wystarczy aby w pełni przedstawić metodę
bo masz tutaj rozważony tylko jeden przypadek
Sposób rozwiązywania masz tutaj
http://matwbn.icm.edu.pl/ksiazki/mon/mon11/mon1110.pdf
Równanie trzeciego stopnia masz też w zbiorze Krysickiego i Włodarskiego
razem z przykładami wziętymi z geometrii w jednym zadaniu odwołują się też do
jednego z praw fizyki poznawanego już w szóstej klasie
Ten wątek pokazuje że pomocy raczej nie znajdziesz na forach
7 mar 19:14
Mariusz:
Kati20 tak naprawdę to wskazówka PW jest trochę nie na temat
Gdyby chodziło o metody numeryczne to zadanie byłoby inaczej sformułowane
7 mar 19:28
Mariusz:
ABC przypominasz mi kolesia który po youtubach nazywa siebie
Norman J Wildberger który twierdzi że liczby niewymierne nie istnieją
Gdyby jego twierdzenia były prawdziwe obalałoby to całą analizę matematyczną
7 mar 19:40
ABC:
Mariusz co do istnienia to przypomniało mi się powiedzenie:
"Bóg istnieje bo matematyka jest niesprzeczna. Istnieje też diabeł, bo nikt nie potrafi tego
udowodnić."

7 mar 20:16
PW: Mariusz, widzę że masz uczulenie na mnie. Patrz, wskazówka była "nie na temat", a
Kati20 podziękowała, że już wie co ma zrobić.
Dobrze, że opanowałeś rozwiązywanie równań trzeciego stopnia, ale... Jest to śmiertelnie nudne,
odtwórcze i nikomu nie jest potrzebne. Co ma zrobić człowiek z informacją, że
x=3√24+16p[2}+3√24−16√2+4
− wziąć kalkulator i policzyć przybliżenie, żeby jakoś tę liczbę umiejscowić na osi?
7 mar 21:59


 Równanie 3−stopnia musi mieć przynajmniej jeden pierwiastek
Równanie 3−stopnia musi mieć przynajmniej jeden pierwiastek
 zys no to rozwiązuj, ja popatrzę czy jesteś tak dobry jak Mariusz
zys no to rozwiązuj, ja popatrzę czy jesteś tak dobry jak Mariusz 


