Nie umiem dalej nic

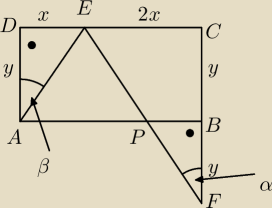
Nie umiem dalej nic Maciess: rysunek

Dany jest prostokąt ABCD. Na boku CD tego prostokąta wybrano taki punkt E, że |EC|=2|DE|, a na przedłuzeniu boku CB wybrano taki punkt F, ze |BF| = |BC|. Niech P oznacza punkt przecięcia prostej EF z prostą AB (zobacz rysunek). Wykaz, że trójkąty AED i PFB są przystające. ΔAED i ΔPFB są prostokątne. Pozostałe kąty musza być ostre.

	2x		x		x
tg α =		=		tg β =
	2y		y		y

tg α=tg β ⇒ α=β Trojkąty mają po dwa takie same kąty więc 3 muszą mieć również identyczny. Są więc podobne (KKK). ΔAED~ΔPFB |DE|=x

	\|EC\|		\|CF\|
ΔECF~ΔPFB więc		=
	\|PB\|		\|BF\|

2x		2y
	=
\|PB\|		y

|PB|=x |PB|=|DE| Trójkąty są podobne, a para odpowiadających sobie boków ma takie same miary więc trójkąty sa przystające. Czy to jest poprawne? Zadanie z próbnej matury zadania.info

6 mar 20:11

iteRacj@: Zgadza się. Krócej jest skorzystać z tw.Talesa dla prostych EF i CF. Wtedy od razu |PB|=x i z cechy (bkb) masz przystawanie ΔAED i ΔPFB.

6 mar 20:24

iteRacj@: Tytuł dałeś mało optymistyczny, ale też mogę się pod nim podpisać...

6 mar 20:25

Maciess: No nie jestem urodzonym optymistą, nic nie poradze. https://pdf.zadania.info/63481.pdf Wrzucam link do całego arkusza, moze komus sie przyda. I jestem ciekaw waszej opinii, bo wg mnie ciut trudniejszy niz Nowa Era/Operon. (na razie zrobiłem tylko podstawe)

6 mar 20:43

iteRacj@: Masz jakieś udziały w tych kwotach? : )

6 mar 20:55

Maciess: A skąd zapomniałem o tym

https://pdf.zadania.info/77440.pdf ten link powinien działać

6 mar 21:04

iteRacj@: Teraz to innego, ale czy to zgodne z prawem?

6 mar 21:08

iteRacj@: *co innego

6 mar 21:08

Maciess: Podałem link ogólnodostepny, dostepny dla kazdego na ich stronie. Wczesniej podałem taki, który wygenerowało dla mnie, jako uzytkownika zalogowanego na ich forum ( z dodatkowym dostępem czy jakims abonamentem) − dlatego wyrzuca błąd i "prośbe o okup". Więc wszystko jest legalne, mozna przeglądać i panowie w czarnych płaszczach nie powinni sie zjawić emotka

6 mar 21:13

Eta: zad33 Podaję taki sposób rozwiązania tego zadania f−e=14 , 4a=68 ⇒ a=17

	fe
f²+e²=4a² ⇒ (f−e)²+2fe=4a² ⇒ 196+2fe=4*289 /: 4 ⇒		=P= 289−49
	2

P=240 =======

6 mar 21:15

Eta: Zadanie 33 z profilu podstawowego

6 mar 21:17