Styczna do wykresu, pochodne Kamila : Wykaż że styczna do wykresu funkcji f(x) =x3+2x2−6x+1 w punkcie p=(1, − 2) ma z tym wykresem jeszcze jeden punkt wspólny.

wredulus_pospolitus: 1) wyznaczasz wzór stycznej (h(x)) z wykresem f(x) w punkcie P 2) wyznaczasz rozwiązania równania f(x) = h(x)

Kamila : Dzięki!

wredulus_pospolitus: Możesz też zrobić 'dowód', wtedy musiałbyś: 1) wykazać, że styczna nie będzie postaci x=a 2) wykazać, że f(x) 'maleje szybciej' w x−> −∞ niż jakakolwiek styczna 3) wykazać, że f(x) 'rośnie szybciej' w x−> +∞ niż jakakolwiek styczna Jednak wydaje mi się, że wyznaczenie tej stycznej będzie dla Ciebie o wiele łatwiejszym problemem.

janek191: f '(x) = 3 x² + 4 x − 6 f '(1) = 3 + 4 − 6 = 1 y = x + b P = ( 1, − 2) − 2 = 1 + b ⇒ b = − 3 y = x − 3 ======= x³ +2 x² − 6 x + 1 = x − 3 x³ +2 x² − 7 x + 4 = 0 x = 1 x³ + 2 x² − 7 x + 4 = ( x −1)*(x² +3 x − 4) = ( x −1)*( x +4)*(x − 1) Punkt wspólny R = ( − 4, 26) ===========

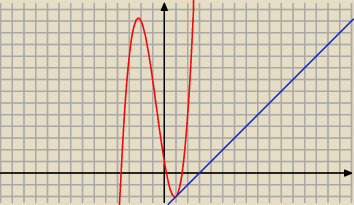
janek191: Pomyłka: R = ( − 4, − 7)