Prostokat
6latek:
| | AB | |
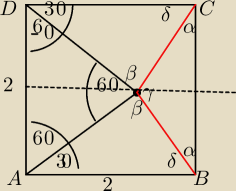
Dany jest prostokat ABCD w ktorym |
| = U{√3+1{2} i taki punkt P nalezacy do danego |
| | AD | |
prostokata
ze trojkat ADP jest rownoboczny . Oblicz miary katow trojkata BPC
Z tresci zadania wychodzi ze to bedzie kwadrat
δ= 90−α
β= 180−30−(90−α)
β=60−α
γ=360−60−(60−α)−(60−α)
γ= 180+2α a to wyszla mi bzdura
6 mar 12:35
bezendu: Bzdura do bzdury i mamy dwie bzdury
6 mar 12:37
6latek: Czesc
Widze ze tluczesz rownania rozniczkowe
6 mar 12:40
bezendu:
Niemcy mnie męczą to tukę
6 mar 12:40
6latek: Juz dlugo jestes tam ?
6 mar 12:41
janek191:
@ Bezendu:
Nie dawać się Niemcom
6 mar 12:42
bezendu:
6latek, niedługo, ale wiem, że długo tam zostanę
6 mar 12:44
6latek: Witaj
Janek191
Pomozesz .
6 mar 12:44
6latek: Mnie tez szykowalo ale moze wroce do pracy
6 mar 12:45
6 mar 12:46
6latek: | | aB | | √3+1 | |
Pisze w zbiorze tak |
| = |
| |
| | AD | | 2 | |
6 mar 12:47
bezendu:
W zbiorze jest napisane tak*
6 mar 12:53
ite: zgubiony plus
β= 180−30−(90−α)
β=60+α
6 mar 13:05
6latek: Dzien dobry
Powiedz mi czy podany stosunek ma tutaj znaczenie do obliczen czy tylko podany z eby
zorientowac sie ze to kwadrat
6 mar 13:09
ite:
Dzień dobry!
Czy tam rzeczywiście jest 2/2=1?
Miary kątów ΔBPC zależą od proporcji między bokami prostokąta. Wynik obliczeń zależy od tej
proporcji (a nie od długości boków).
6 mar 13:14
6latek: γ= 360−60−(60+α)−(60+α)
γ= 180−2α
Na razie stoje z zadaniem
6 mar 13:14
6latek: Tak jest napisane
Jesli masz zbior Drobka Szymanski Zbior zadan z geometrii dla klasy 1 i 2 liceum
ogolnoksztalcacego (ja mam z 1998r) to jest to zadanie 1. 102
6 mar 13:17
ite:
Z tego, co napisałeś 12:47, wynika, że boki są równe, ale nie można wyciągnąć wniosków jaką
mają długość.
6 mar 13:17
6latek: Czyli tak ak na poczatku myslalem ze podany stosunek sluzy do wyciagniecia wniosku ze tylko
boki sa rowne
6 mar 13:19
ite:
Ci dwaj panowie to moi dobrodzieje, za pomocą tego zbioru nauczyli mnie geometrii
Pozdrów
ich ode mnie.
Załóż, że |AB|=|AD|=a
Oblicz wysokość ΔADP, potem wysokość czerwonego Δ. Jego podstawa też ma długość a.
I z funkcji trygonometrycznych znajdziesz γ i α.
6 mar 13:24
6latek: OK
6 mar 13:27
6latek: ite
Bedziesz gdzies za 2 godzinki na forum ?
Teraz musze isc na spacer bo wczoraj nie bylem a tak byc nie moze .
6 mar 13:52
ite:
To zajrzę i podpowiem, jak będą jakieś wątpliwości.
Mój wynik to α=15o
6 mar 13:58
6latek: Odpowiedz to 45o,45o, 90o
6 mar 15:30
ite: | | |AB| | | √3 + 1 | |
Taki wynik jak 15:30 otrzymamy, jeśli |
| = |
| . |
| | |AD| | | 2 | |
6 mar 15:34
6latek: Dobrze bede liczyl tak jak podpowiadalas
6 mar 15:46
Mila:
bezendu i co tam robisz? Uczysz się, pracujesz?
6 mar 19:27
6latek: Dobry wieczor
Milu
Zrobilem to zadanie i nastepne tez
6 mar 19:45
6latek: iteRacjo
z 1 zadania 1 wysokosc mi wyszla √3 stad druga wysoksc wuyszla 1
Ztego wyciagam wniosek ze drugi trojkat to trojat prostokatny rownoramienny
6 mar 20:00
iteRacj@:
Nie wiemy, jaką długość mają boki tego prostokąta, znamy tylko proporcję między nimi.
| | √3+1 | | √3+1 | |
Czy w Twoich obliczeniach ta proporcja wynosi tak jak napisałeś |
| czy |
| |
| | 2 | | 2 | |
tak jak wynika z odpowiedzi?
6 mar 20:17
6latek: ta druga i wzialem dugosc AD=2 i AB= √3+1
6 mar 20:33
iteRacj@:
I wszystko się zgadza. Można zaczynać następne zadania.
6 mar 20:43
6 mar 20:44
bezendu:
Mila studiuję i pracuję. Nie mam zamiaru wracać nawet
6 mar 21:28
6 mar 21:41
bezendu:
Cześć
Eta oczywiście, że pamiętam
6 mar 21:43
