pole vvool: Najdłuższy bok trójkąta ma długość 3, najkrótszy długość 1. Jakie jest największa pole trójkąta, spełniającego te warunki?

Adamm:

	3*1
P =		*sinα, α − kąt pomiędzy
	2

największe pole będzie dla sinα = 1, czyli trójkąta prostokątnego wtedy P = 3/2

Eta:

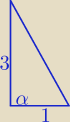
	1
P=		*3*1*sinα −− jest największe gdy sinα=1 czyli gdy α=90o
	2

	3
P=
	2

wredulus_pospolitus: ekhm ... a od kiedy w tym momencie najdłuższym bok będzie miał długość 3

wredulus_pospolitus: Największe pole będzie dla trójkąta równoramiennego o ramiona równych 3

	√35
Wysokość wynosi
	2

	√35
Więc pole to: P =
	4

Eta: I tym razem "wrednusie" masz 100% racyjii

vvool:

	3
Czyli jak dobrze zrozumiałem gdy najdłuższy bok jest równy 3 to największe pole to		,
	2

natomiast

	√35
w moim zadaniu		?
	4

Eta: Patrz odp; "wredn......... sa"

Eta: Adamm ....... ja

wredulus_pospolitus: Argumentacja, dlaczego taki trójkąt będzie miał największe pole (przy zadanych warunkach): Należy zauważyć, że w takim trójkącie równoramiennym 'środkowy' (co do długości) bok będzie równy najdłuższemu, tak więc kąt pomiędzy 'najkrótszym i najdłuższym' bokiem będzie największy. To w połączeniu ze wzorem na pole trójkąta przypomnianym przez Adamma pokazuje, że właśnie wtedy pole będzie największe.

vvool: ok dziękuje wam

Adamm: To może tak. Ze wzoru Herona 16P² = (4+x)(4−x)(−2+x)(2+x) = (16−x²)(x²−4), 1≤x≤3 16P² przyjmuje maksymalną wartość dla x = 3 16P² = 7*5 = 35

	√35
P =
	4