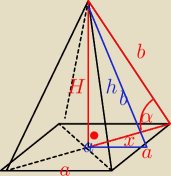
Ostrosłup prawidłowy czworokątny oblicz pole sciany bocznej ;--D: Dany jest ostrosłup prawidłowy czworokątny o objętości 64. Tangens kąta nachylenia krawędzi ściany bocznej do krawędzi podstawy jest równy 3√2. Wyznacz pole dowolnej ściany bocznej tego ostrosłupa. Mógłby ktoś pomóc? Wychodzą mi dziwne liczby typu wysokość ostrosłupa 24³√2 Dzięki

xyz:

	a√2
x =
	2

	H
tg α =
	x

H
	=3√2
x

	a√2		3*2*a
H = 3√2x = 3√2*		=		= 3a
	2		2

1
	a2*3a = 64
3

a³ = 64 a=4 H = 12 x = 2√2 (a/2)²+H²=h_b² 4 + 144 = h_b² h_b=√148 = √4*37 = 2√37

	1		1
P =		a*hb =		*4*2√37 = 4√37
	2		2

Eta: Nie ten kąt α ?

xyz: krawędzi bocznej do podstawy to ten, który zaznaczyłam możliwe, że −−D zaznaczył inny

Eta: W treści jest .......... " krawędzi bocznej do krawędzi podstawy"