Planimetria Hali: Długości boków trójkąta tworzą ciąg arytmetyczny a najkrótszy bok ma długość 3 jeżeli największy kąt ma 120° to pole wynosi?

wredulus_pospolitus: z tw. cosinusów: (3+2r)² = 3² + (3+r)² − 2*3*(3+r)*cos120^o wyznaczasz 'r'

	1
później np. z P =		*3*(3+r)*sin120o
	2

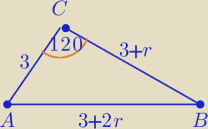
Mila: r>0 Z tw. cosinusów: (3+2r)²=3²+(3+r)²−2*3*(3+r)*cos(120^o) 9+12r+4r²=9+9+6r+r²+9+3r 3r²+3r−18=0/:3 r²+r−6=0, r>0 Δ=25

	−1−5		−1+5
r=		<0 lub r=		=2
	2		2

r=2 Boki Δ: 3, 5, 7

	1		15		√3
PΔ=		*3*5*sin(120o)=		*
	2		2		2

	15√3
PΔ=
	4

===========