Wyznacz wspolrzedne wierzcholka A (rownoleglobok,wektory)
Wyznacz:
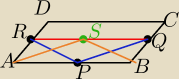
Punkty P = (−3, −9), Q = (8, 4) i R = (−12, −4) sa srodkami odpowiednio boków AB, BC
i DA równoległoboku ABCD. Wyznacz współrzedne wierzchołka A tego równoległoboku.
Nie wiem czy mój sposób jest dobry,więc jeśli nie jest to prosiłbym o rozwiązanie tego zadania.
ΔRPQ jest równoramienny,wyznaczam S ze wzoru na środek odcinka RQ,bo są podane punkty.
|SA|=|SB| z wektorów,wyznaczam z tego x
b,y
b i liczę x
a,y
a ze wzoru na środek odcinka |AB|
Czy jest to poprawne?
5 mar 15:46
wredulus_pospolitus:
Propozycja 1:
1) wyznaczasz równanie prostej zawierającej RQ
2) wyznaczasz równanie prostej równoległej z (1) ale przechodzącej przez P
3) obliczasz |RQ|
| | |RQ| | |
4) wyznaczasz punkt na prostej (2) odległy o |
| od punktu P |
| | 2 | |
5) w ten sposób masz współrzędne punktu A i B
5 mar 15:53
Wyznacz: dzięki,a to co podałem jest źle?
5 mar 15:53
wredulus_pospolitus:
Propozycja 2:
1) wyznaczasz równanie prostej zawierającej RQ
2) wyznaczasz równanie prostej równoległej z (1) ale przechodzące przez P
3) wyznaczasz równanie prostej PROSTOPADŁEJ do (1) i (2), przechodzącej przez R
4) przecięcie się prostych (2) i (3) to szukany punkt A
5 mar 15:54
wredulus_pospolitus:
|SA| = |SB| <−−− okey ... ale jaka jest długość? (ja wiem, Ty pewnie też ... ale o tym nie
piszesz nigdzie)
Można tak zrobić (o ile wiesz ile wynosi |SA| ) ale szczerze mówiąc jest to mocno skomplikowane
podejście i nadal potrzebujesz (tak jak przy propozycji 1) ustalić który z wyznaczonych
punktów to A, a który to B
5 mar 15:58
wredulus_pospolitus:
a nie ... nie będzie tak łatwo to zrobić u Ciebie ... za każdym razem będziesz musiał sprawdzać
czy warunek, że P jest środkiem odcinka AB jest spełnione czy też nie
5 mar 15:59
Wyznacz: znaczy nie chodzi mi o dlugosc,tylko o wektory,zle to ujalem bo znaku wektora nie moglem
znalezc

. Wektor SA = Wektor SB
5 mar 16:01
jc: P = (−3, −9), Q = (8, 4) i R = (−12, −4)
| | 1 | |
A = P + |
| (R−Q) = ... wystarczy podstawić ... |
| | 2 | |
5 mar 16:02
jc: | | 1 | |
A=(−3,−9) + |
| ( (−12, −4) − (8,4) ) = (−3,−9) + (−10, −4) = (−13, −13) |
| | 2 | |
5 mar 16:04
Wyznacz: Dzieki za pomoc
5 mar 16:05
 Punkty P = (−3, −9), Q = (8, 4) i R = (−12, −4) sa srodkami odpowiednio boków AB, BC
i DA równoległoboku ABCD. Wyznacz współrzedne wierzchołka A tego równoległoboku.
Nie wiem czy mój sposób jest dobry,więc jeśli nie jest to prosiłbym o rozwiązanie tego zadania.
ΔRPQ jest równoramienny,wyznaczam S ze wzoru na środek odcinka RQ,bo są podane punkty.
|SA|=|SB| z wektorów,wyznaczam z tego xb,yb i liczę xa,ya ze wzoru na środek odcinka |AB|
Czy jest to poprawne?
Punkty P = (−3, −9), Q = (8, 4) i R = (−12, −4) sa srodkami odpowiednio boków AB, BC
i DA równoległoboku ABCD. Wyznacz współrzedne wierzchołka A tego równoległoboku.
Nie wiem czy mój sposób jest dobry,więc jeśli nie jest to prosiłbym o rozwiązanie tego zadania.
ΔRPQ jest równoramienny,wyznaczam S ze wzoru na środek odcinka RQ,bo są podane punkty.
|SA|=|SB| z wektorów,wyznaczam z tego xb,yb i liczę xa,ya ze wzoru na środek odcinka |AB|
Czy jest to poprawne?
 . Wektor SA = Wektor SB
. Wektor SA = Wektor SB