Graniastosłup Xvartis: Podstawą graniastosłupa prostego jest równoległobok o bokach 4 i 6 oraz kącie 60 stopni. Wiedząc że krótsza przekątna ma długość 4√3, oblicz pole powierzchni bocznej tego graniastosłupa.

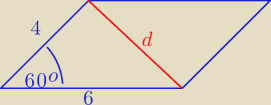
janek191: Z tw. kosinusów. d² = 6² + 4² − 2*6*4*cos 60^o = 36 + 16 − 24 = 28 Z tw. Pitagorasa h² + d² = ( 4√3)² h² = 48 − 28 = 20 = 4*5 więc d = 2√5 Pole P_b = ( 2*6 + 2*4)*h = 20*2√5 = 40 √5 j²