twierdzenie sinusow i cosinusow MacinMacin: Rozwiąż trójkąt ABC mając dane: ∡ABC=120 stopni oraz AB = 2√3 i AC=6 mógłby ktoś pomóc to rozwiązać ale z dobrym wytłumaczeniem bo nic z tego nie rozumiem

wredulus_pospolitus: Kuźwa ... co niby oznacza 'rozwiąż trójkąt' Co on ... związany sznurkiem jest

MacinMacin: nie wiem sam nie wiem o co chodzi nie mam rysunku tylko takie polecenie to wszystko

wredulus_pospolitus: Polecenie masz: "rozwiąż trójkąt" To jest polecenie z książki czy tak sobie zapisałeś w zeszycie?

Mila: Rozwiąż trójkąt⇔obliczyć miary kątów i boków.

6latek: wredulusie sa takie polecenia .

MacinMacin: mam wpisane na kartce co dostałem od nauczyciela takie zadanie nie ma żadnego obrazka jak napisałem wyżej

6latek: dzien dobry Milu Kolego rysunek zrob sobie sam

Mila: Witam Cię miło

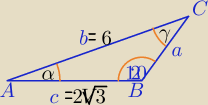
Mila: 1) Z tw. sinusów:

6		2√3
	=		⇔6*sinγ=2√3*sin(120o)
sin(120o)		sinγ

	√3
sin120=sin(180−60)=sin60=
	2

	√3
6*sinγ=2√3*
	2

6sinγ=3

	1
sinγ=		⇔γ− kąt ostry,
	2

γ=30^o 120+30+α=180 α=30⇔ΔABC jest trójkątem równoramiennym a=|BC|=|AB|=2√3 odp. Kąty: 120^o,30^o,30⁰ boki: 6, 2√3,2√3