Czworościan foremny ABCD
Xvartis: Dany jest czworościan foremny ABCD. Punkt E jest środkiem krawędzi CD. Pole trójkąta ABE jest
równe 75√2.Wyznacz długość krawędzi czworościanu ABCD.
4 mar 16:38
Mila:
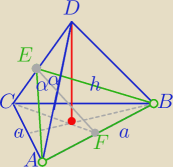
1)
W ΔBFE:
| | 1 | | 2 | | √2 | |
sin2α=1− |
| = |
| ⇔sinα= |
| |
| | 3 | | 3 | | √3 | |
| | 1 | | √2 | | 2√2 | |
sin2α=2* |
| * |
| = |
| |
| | √3 | | √3 | | 3 | |
| | 1 | | 1 | | 3a2 | | 2√2 | |
2) PABE= |
| *h2*sin(2α)= |
| * |
| * |
| =a2√2 |
| | 2 | | 2 | | 4 | | 3 | |
a
2√2=75
√2
a
2=75
a=5
√3
==========
4 mar 20:28
ks: Pole będzie wynosić 14a2√2
Czyli a=10√3
19 kwi 11:12
α&β:
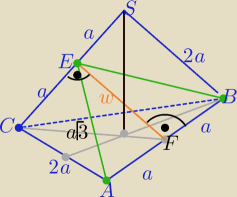
Z tw. Pitagorasa w ΔCEF
w
2=(a
√3)
2−a
2 ⇒ w=a
√2
P(ABE)= a*w =75
√2 ⇒ a
2=75 , a>0
a=5
√2
to długośći krawędzi czworościanu:
2a=10
√2
========
i po ptokach
19 kwi 12:34
α&β:
Sorry za chochlika a= 5√3
to 2a= 10√3
==========
19 kwi 12:35
chichi:
α&ω
19 kwi 12:39
α&β:
No to jesteś lepszy ode mnie
19 kwi 12:51
Mila:
19 kwi 23:35