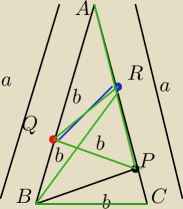
Trojkat rownoramienny 6latek: Trojkat rownoramienny ABC w ktorym AB = AC ma nastepujaca wlasnosc Na ramieniu AC mozemy znalezc takie punkty P i R a na ramieniu AB taki punkt Q ze |BC|=|BR|=|RQ|=|QP|=|PA|. Oblicz miary kątow trojkata ABC Jak sie za to zabrac? b= odcinki rowne BC

wredulus_pospolitus: Zauważ, że: ΔCBR jest równoramienny tak samo ΔPQR Tak więc: ∡BCR = ∡CRB = α ∡QPR = ∡PRQ = β Zauważ, że: α = ∡BCR > ∡QPR = β natomiast: β = ∡QRP > ∡BRC = α No i mamy sprzeczność

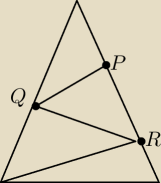
6latek: Tresc zadania dobra ale rysunek do zadania jest zly (sam go robilem ) Tak ma byc Odpowiedz to 80,80,20

wredulus_pospolitus: To na spokojnie popatrz gdzie masz trójkąty równoramienne i pokoloruj 'równe kąty'

6latek: Tak zrobie . Moze jeszcze przy okazji pokoloruje drwala

an: ∡BAC=∡AQP=α ...... ∡RBC=α ∡BRC=∡RCB=4α 9α=180 α=20

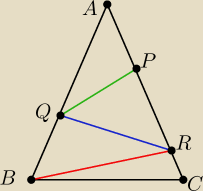
6latek: Bedziemy mieli takie trojkaty rownoramienne 1) ΔAQP 2) PQR 3) QRB 4) RBC

ite: zał. |<BAC|=α

	180o−α
z ΔABC: |<ACB|=|<ABC|=		=90o−α/2
	2

ΔRBC równoramienny ⇒ |<BRC|=|<ACB|=90^o−α/2 i |<RBC|=180^o−180^o+α/2+α/2=α ΔAPQ równoramienny ⇒ |<AQP|=|<BAC|=α i |<APQ|=180^o−2α więc |<QPR|=180^o−|<APQ|=2α ΔQPR równoramienny ⇒ |<PRQ|=2α i |<PQR|=180^o−4α więc |<RQB|=180^o−α−(180^o−4α)=3α ΔQRB równoramienny ⇒ |<QBR|=3α |<ABC|=|<QBR|+|<RBC|=3α+α=4α |<ABC|=4α suma kątów ΔABC 9α=180^o czyli to co napisał an znacznie krócej

6latek: dzien dobry Za chwile bede pisal .Odpoczne troche bo wrocilem z dlugiego spaceru

ite: Dzień dobry! Chyba najłatwiej będzie zrobić na kartce duży rysunek i powpisywać wielkości kątów, na ekranie trudno się to czyta. Można ułożyć końcowe równanie tak jak an ale spróbuj też przyrównać miary kątów przy podstawie w ΔABC.

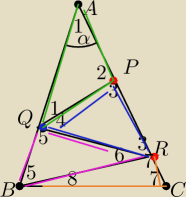
6latek: Zrobie jeszcze raz rysunek Chcialem to zrobic tak Kąt nr 1 =α stad kat nr 2 = 180−2α stad kąt nr 3= 180−(180−2α)= 2α stad kąt nr 4 = 180−4α kąt nr 5= 180−(180−4α)−α= 4α−α=3α Kat nr 6= 180−6α kat nr 7= 180−(180−6α)−2α= 4α Stad kąt nr 8= 4α−3α=α Wiec 4α+4α+α= 9α 9α=180⇒α=20^o 4α= 80^o