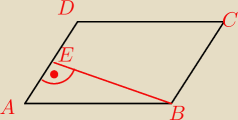
Przekątne równoległoboku Karolinkaa: Czworokąt na rysunku jest równoległobokiem |AE|=2; |ED|=2; |AB|=12 Oblicz długość przekątnych tego równoległoboku. Bardzo dziękuję za pomoc.

PW: Wyliczenie |EB| jest możliwe z twierdzenia Pitagorasa. Mając |EB| wyznaczany cosA. Twierdzenie kosinusów zastosowanew w ΔDBA pozwala wyliczyć |BD|.

PW: A właściwie cosA wyznacza się bez znajomości |EB|

Karolinkaa: a jak ten cosinus wyciagnac

PW: Kąt A jest kątem w trójkacie prostokątnym BED − zastosować definicję.

wredulus_pospolitus:

	2
cos B =
	12

A = 180 − B

	2
więc cos A = cos(180 − B) = −cos B = −
	12

PW: W trójkącie BEA, zmęczony jestem, przepraszam.

kuba: To może nie odpowiadaj jak jesteś zmęczony, aby nie wprowadzać innych w błąd?

Karolinkaa: bo z podobieństwwa trójkątów bym poprostu dała że BD = 12 ale AC mi brakuje

Karolinkaa: czy dłuższa to c²=12²+4²−2*12*4*cosB i cos B to −2/12 ?

ICSP: ΔAEB ≡ ΔEBD ( kbk) ⇒ |BD| = |AB| Aby policzyć drugą : 1. Liczysz wysokość opuszczoną na AB 2. Z wierzchołka c opuszczasz wysokość na podstawę AB. Przecina ona prosta będącą przedłużeniem odcinka AB w punkcie F 3. Z twierdzenia Pitagorasa liczysz |BF| 4. Z twierdzenia Pitagorasa liczysz |AC|

wredulus_pospolitus: no i AC wyliczysz z tw. cosinusów a cos (∡ABC) to cos(A) z postu 23:13

PW: kuba, najgorsze są na forum te ścierwa, co innym nie pomogą, ale czyhają żeby komuś wbić szpilę. A nie zauwazyłeś, mądralo, że wredulus też się pomylił?

Karolinkaa: cos(A)=cos(B)?

wredulus_pospolitus:

	2
cos(∡BAE) =
	12

	2
cos(∡ABC) = cos(180 − ∡BAE) = −cos(∡BAE) = −
	12