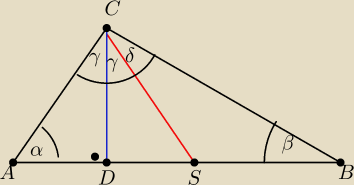
TRojkat 6latek: W trojkacie ABC dlugosc srodkowej CS jest rowna 1/2 AB a wysokosc porowadzona a wierzcholka C zawiera sie w dwusiecznej kąta ACS Oblicz miary katow trojkata ABC Do czego doszedlem AS= 1/2 AB AD+DS= CS stad ΔACS to Δ rownoramienny czyli α= 2γ No chyba z e z tegp skorzystac ze srodkowa dzieli trojkat na dwa trojkaty o rownych polach

Pytający: W ΔADC masz, że α=90−γ oraz wiesz ze α=2γ Dalej będzie z górki

6latek: Ja nawet nie wiem czy ten trojkat ACS nie jest rownoboczny Bo AS= CS a jesli wysokosc zawiera sie w dwusiecznej to jest cecga trojkata rownoramiennego a takze rownobocznego czyli mialbym α= 60^o γ= 30^o 2γ= 60^o JUz widze trojkat BSC test rownoraniemienny Kat BSC= 120^o Wobec tego β=δ i maja po 30^o Bedzie to trojkat prostokatny 60^o , 90⁰ 30^o. Prosze sprawdzic . ZA chwile odpowiem bo musze wyjscv po wegiel

6latek:

yyy:

6latek: Cos wiecej na ten temat moge prosic?

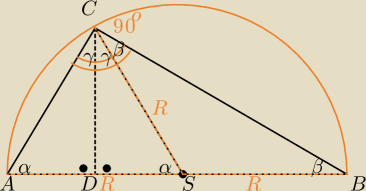
yyy: |AS|=|CS|=R, ΔCDA∼ΔCDS /kkk/ |AC|=|CS| ↓ ΔACS równoboczny

yyy: 18:13 A,B,C są równoodległe od pkt S ↓ leżą na okręgu o promieniu R=|AS| i środku S |AB|=2R ↓ AB jest średnicą tego okręgu ↓ ABC to trójkąt prostokątny

6latek: To rozumiem

yyy: α+γ=90^o z ΔADC α+β=90^o z ΔABC ↓ β=γ (γ+β)+β=90^o z ΔCDB 3β=90^o ↓ β=30^o γ=30^o α=2γ=60^o

6latek: Dzieki wielkie za takie poswiecenie