monotoniczność ciągu Whale: Zbadaj monotoniczność ciągu:

	n+1
an = ln
	n

zaczynam tak:

	n+2
an+1 = ln
	n+1

	n+2		n+1		(n+2)*n
an+1 − an = ln		− ln		= ln
	n+1		n		(n+1)2

jak to dalej ugryźć?

janek191:

n2 + 2n
	< 1
n2 + 2 n + 1

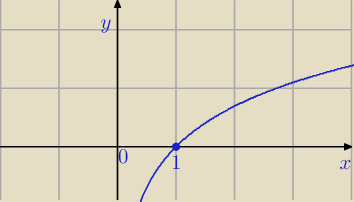
więc

	n2 + 2n
ln		< 0
	n2 + 2 n + 1

Whale: Mogę jeszcze zapytać jak sprawdzić monotoniczność takiego ciągu rekurencyjnego? a₁ = 2 a_n+1 = a_n + 2* 10ⁿ⁻¹ Myślałem o indukcji, 1. a₁ < a₂ 2. a_n−1 < a_n => a_n < a_n+1 3. Tylko jak przeprowadzić obliczenia, aby dojść do takiego wniosku?

janek191: a_n+1 − a_n = 2*10ⁿ⁻¹ > 0