Trzeci bok trójkąta-geometria analityczna. Kę: Proste o równaniach 3x−2y+2=0 i x−y+2=0 zawierają dwa boki pewnego trójkąta, a prosta o równaniu 2x− y−1=0 zawiera jedną z jego środkowych. Znajdź równanie prostej zawierającej trzeci bok trójkąta. Znalazłem jedną prostą 5x−3y=0 a w odpowiedzi jest jeszcze x−4=0. Jak zrobić drugi przypadek? Kombinowałem, ale nie wychodzi mi to

janek191: Czy dobrze przepisana jest treść zadania?

Kę: Tak, treść zadania jest przepisana dobrze.

wredulus_pospolitus: to pokaż jak wyliczyłeś/−aś pierwszy przypadek Zauważ, że 2x−y−1 = 0 (dzięki które wyznaczamy środek boku leżącego na jednej z podanych prostych) przecina zarówno jedna prostą jak i drugą prostą −−−− więc tutaj masz te dwa przypadki

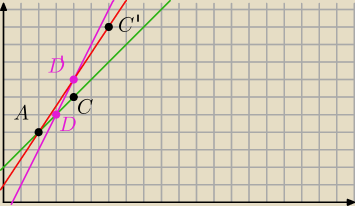
wredulus_pospolitus: Przypadek 1: punkt D jest środkiem boku trójkąta, wtedy: D' = B (wierzchołek trójkąta) C jest drugim wierzchołkiem wyznaczasz prostą zawierającą D'=B i C (i tego przypadku nie zrobiłeś/−aś) Przypadek 2 punkt D' jest środkiem boku trójkąta, wtedy: D = B (wierzchołek trójkąta) C' = C (drugi wierzchołek trójkąta) wyznaczasz prostą zawierającą D=B i C'=C (a to zrobiłeś−aś)

Kę: Okej, już rozumiem, dzięki wielkie !