Stereometria graniastosłupy
Wiktoria: Witam proszę o pomoc z tymi trzema zadaniami z graniastosłupów. Jeśli można prosić
potrzebowałbym rozwiązania dzisiaj.
Z góry dziękuje za pomoc
1. Jaki kąt tworzy przekątna ściany bocznej graniastosłupa prawidłowego trójkątnego o długości
12 z krawędzią podstawy, jeżeli promień okręgu opisanego na podstawie tego graniastosłupa ma
długość 6
2. Oblicz objętość i pole powierzchni bocznej graniastosłupa prawidłowego sześciokątnego,
którego krótsza przekątna ma długość 4V3, a wysokość graniastosłupa jest trzy razy dłuższa od
podstawy
3. W graniastosłupie prawidłowym czworokątnym przekątna o długości 10 cm jest nachylona do
podstawy graniastosłupa pod takim kątem α, że sin α = 0,2 . Oblicz objętość i pole powierzchni
całkowitej owego graniastosłupa
3 mar 00:32
janek191:
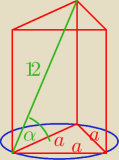
r = 6
Z tw. kosinusów:
a
2 = r
2 + r
2 − 2 r
2 cos 120
o = 72 − 72*cos( 90
o + 30
o) = 72 − 72*( −0,5) = 72 + 36 = 108
a
2 = 36*3
a = 6
√3
zatem
α = 60
o
=======
3 mar 08:29
janek191:
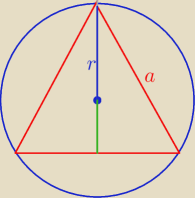
3 mar 13:19
janek191:
Bez tw. kosinusów.
cd.
2*1,5 r = a
√3
3 r = a
√3 / :
√3
a =
√3 r = 6
√3
================
3 mar 13:21
janek191:
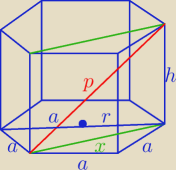
z.2
Mamy p = 4
√3
h = 3 a
r = a
oraz
x
2 + a
2 = 4 r
2 = 4 a
2
x
2 = 3 a
2
Tw. Pitagorasa
p
2 = x
2 + h
2 = 3 a
2 + (3 a)
2 = 3 a
2 + 9 a
2 = 12 a
2
( 4
√3)
2 = 12 a
2
48 = 12 a
2
a
2 = 4
a = 2
=====
h = 3 a = 6
==========
| | a2√3 | |
V = Pp*h = 6*PΔ *h = 6* |
| *h =1,5 a2 √3*h = 1,5*4*√3*6 = 36√3 j3 |
| | 4 | |
P
c = 2 P
p + 6 a*h =
gdzie
P
p = 1,5 a
2 √3
3 mar 13:38
Wiktoria: Dziękuje
3 mar 14:15
Wiktoria: Janek, mógłbym mi wyjaśnić czemu 72* cos120 wyszło −0.5
Bo rozumiem, że te cos120 zawsze wychodzi z tw. kosiunusów, ponieważ mnie nie było w szkole i
tego nie rozumiem.
3 mar 19:25
Wiktoria: Okay cos ze 120 to z tabelki jest to rozumiem. ALe skad sie generalnie wzielo to 120 stopni.
Jest to "stała", która się podstawia w twierdzewniu cosinów. BO na internecie znalazłem to
twierdzenie lecz bez ilosci stopni
3 mar 19:26
janek191:
cos 120o = cos ( 90o + 30o) = − sin 30o = − 0,5
Wzór redukcyjny
cos ( 90o + α ) = − sin α
3 mar 19:28
janek191:
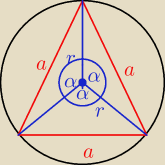
3 α = 360
o ⇒ α = 120
o
3 mar 19:31
Wiktoria: x2 + a2 = 4 r2 = 4 a2
x2 = 3 a2
Skąd to wiadomo? Nie widze nigdzie wlasnosci ktore tak zachodza
3 mar 20:13
janek191:
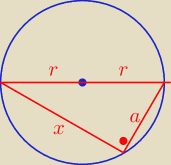
r = a
Tw. Pitagorasa
x
2 + a
2 = ( 2 r)
2 = ( 2 a)
2
x
2 + a
2 = 4 a
2
x
2 = 4 a
2 − a
2 = 3 a
2
x =
√3 a
3 mar 20:24