ee zad: Dziedziną funkcji f(x) jest <−4;1>\{−1} Trzeba określić dziedzinę g(x)=f(x+13), wiem, że jest to przesunięcie o wektor u=[−13;0] i odp zapewne to <−17;−12>\{−14} Tylko jakoś na oko tego nie widzę skoro mam f(x+13) to wydaje się, że to jednak będzie bardziej po prawej stronie nowy wykres niż po lewej. Macie jakąś metodę, żeby to lepiej zobaczyć/zrozumieć?

Eta: Przesunięcie w lewo o 13 jednostek to i dziedzina ( przesunięta w lewo o 13 jednostek zatem D_g= <−7−13, 1−13> = <−17, −12>

Eta: Wrzucił zadanie i zabrał "zad" rozwiązanie ma daleko ..... w "zadzie"

zad: Czemu tak uważasz? Podałem całe zadanie, które miałem na myśli

Jerzy: Jest w języku polskim takie jedno ładne słowo.

Eta:

zad: "wiem, że jest to przesunięcie o wektor u=[−13;0] i odp zapewne to <−17;−12>\{−14}" Po za tym podałem moje rozwiązanie i dalej nie uzyskałem odpowiedzi na moje pytanie.

Eta: co oznacza .....\ {−14}" ?

zad: inaczej zapisane dziedzina to <−17;−14) U (−14;−12>

Eta: Achh .. nie zauważyłam ,że w D_f jest .... /{−1} Odp: D_g=<−7−13, 1−13> /{−1−13} = .......

zad: Ogólnie rozumiem zamysł tego, że trzeba tak przesunąć napisałem nawet " o wektor u=[−13;0]" Tylko, że na oko jakbym miał robić to gdyby mz było np w x=−3, a ja mam mieć nowy wykres f(x+13) to wydaje się jakby to miejsce zerowe było wtedy w x=10 a jednak skoro wektor u=[−13,0] to będzie w x=−3−13=−16 i nie widzę tego na logikę tylko jako czysty wzór który muszę stosować

Jerzy: A skąd ci przyszo do głowy,że miejscem zerowym tej funkcji jest: x = 10 ?

zad: czysto hipotetycznie poza zadaniem

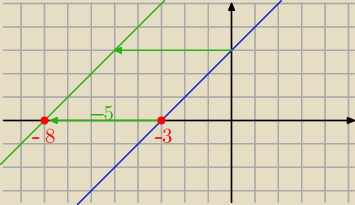
Eta: y=x+3 x_o= −3 g= f(x+5) u=[−5,0] g(x)= (x+5)+3 g(x)=x+8 x_o= −8 = −3−5

Jerzy: To wtedy funkcja f(x + 13) będzie miała miejsce zerowe w punkcie: x = 10 − 13 = − 3

zad: i wszystko stało się jasne dziękuje

Jerzy: Eta , a co ma do tego funkcja y = x + 3 ?

Eta: Dałam inny przykład !

Jerzy: I jak widać, chyba załapał.