Okrąg opisany na trójkącie Zrospaczony: Na okręgu o promieniu 5 są punkty A, B, C. Długosc AC wynoci 6 a długosc BC 8. Oblicz długość AB

Zrospaczony: Próbowałem liczyć z pol ale nie wychodzi

Jerzy: Musisz zauważyć,że ten trójkąt jest prostokątny, a zatem przeciwprostokątna jest średnicą tego okręgu.

Zrospaczony: Ale dlaczego? Jak chcesz to udowodnić

Jerzy: Nie ma tutaj nic do udowadniania. Spostrzegam tylko ,że: trójkąt o bokach 6,8,10 jest prostokątny. 6² + 8² = 10²

6latek: AB= √6²+8²= licz

Zrospaczony: Ehh ale to nie jest wtedy rozwiązanie zadania. Może mieć równie dobrze jeszcze inną możliwość gdzie ten trójkąt jest ostrokątny lub rozwartokątny. Jak udowodnić że takowych nie ma?

Zrospaczony: Mam na myśli trójkąt o bokach 6 i 8 i 3 dowolnym boku

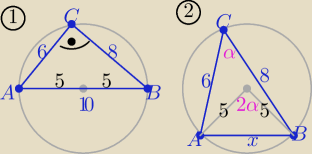
Eta: Z tw. cosinusów x²=6²+8²−2*6*8*cosα i x²=5²+5²−2*5*5*cos(2α) i cos2α= 2cos²α−1 porównując stronami otrzymasz: 100cos²α−96cosα=0 ⇒ cosα=0 v cosα= 0,96 to dla cosα=0 ⇒ α=90^o −− trójkąt prostokątny (1 rys 1) |AB|=10 ( ΔABC prostokątny 2) dla cosα= 0,96 sinα= +√1−0,96² = 0,28 z tw. sinusów

	x
		=2R ⇒x=2,8
	sinα

Odp: |AB|=10 lub |AB|=2,8 ======================

Jerzy: Tylko wtedy promień okręgu opisanego nie będzie równy 5. To jest typowe zadanie na spostrzegawczość.

Jerzy: No, tego drugiego rozwiązania raczej bym nie spostrzegł

Zrospaczony: Dziękuję bardzo Eta

Zrospaczony: Jerzy nie ma zadań z matematyki na spostrzegawczość... Punkty dostajesz za zapisanie rozwiązania pełnego a nie zauważenia że trójkąt prostokątny spełnia warunki zadania. Wtedy z 7 punktów możesz dostać 1 nawet jeżeli jest to dobre rozwiązanie l

Eta:

Eta: "spostrzegawczość" jest bardzo przydatna przy łapaniu pcheł

Jerzy: Bardziej wskazany jest "pośpiech" , ale tutaj mnie zawiódł

Eta: Hej Jerzy zjedz ........

Jerzy: Dziękuję

6latek: Zrospaczony i tu sie mylisz Jest wiele zadan gdzie nalezy zauwazyc pewna prawidlowosc i czy pewien wzor .

Zrospaczony: 6latek ale taka prawidłowości jest np podobieństwo jakichś wielokatów, i bez tego nie zrobisz zadania. Natomiast nigdy zauważenie pasującego do warunków zadania rozwiązania, jak w tym przypadku

Eta: Zrospaczony masz 100% racji !