wymierna
Maciess: Wyznacz wartości parametru m, dla których zbiorem rozwiązan danej nierówności jest przedział
(−2,0)
28 lut 20:49
Pytający:
zał x≠−2
(2−mx−2m)(x+2)>0 pomyśl dalej (rozważ funkcje kwadratową)
28 lut 20:57
Mila:
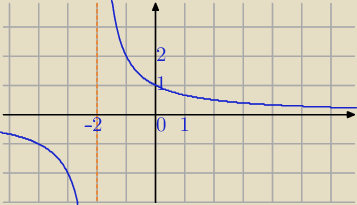
m=1
28 lut 20:59
Mila:
x∊(−2,0)
x+2>0 dla x>−2
−2<x<0 /+2
0<x+2<2
m=1
28 lut 21:03
Maciess:
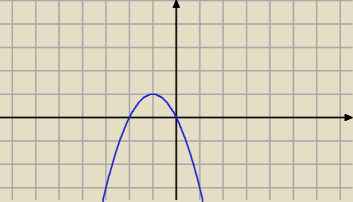
Chciałem uniknąć metody graficznej w tym wypadku wiec.
(2−mx−2m)(x+2)>0
Funkcja musi wyglądac tak miejsa zerowe 0 i −2. −2 mam juz z głowy
−(2−mx−2m)(x+2)<0
(−2+mx+2m)(x+2)<0
−2+mx+2m=0 dla x=0 więc
−2+2m=0 ⇒ m=1
28 lut 21:10
Pytający:
możesz zadać pytanie:
Kiedy iloczyn dwóch liczb jest większy od zera?
28 lut 21:11
Maciess: Kiedy są tych samych znaków.
28 lut 21:16
Pytający: dokładnie, zatem masz
(2−mx−2m>0 i x+2>0 ) lub (2−mx−2x<0 i x+2<0)
28 lut 21:17
Maciess: mx>6x
2
6x
2−mx<0
x(6x−m)<0
6x−m=0 dla x=−2
−12−m=0 ⇒m=−12
Jest dobrze?
28 lut 21:21
Mila:
Wynik dobry.
28 lut 21:48

 Chciałem uniknąć metody graficznej w tym wypadku wiec.
(2−mx−2m)(x+2)>0
Funkcja musi wyglądac tak miejsa zerowe 0 i −2. −2 mam juz z głowy
−(2−mx−2m)(x+2)<0
(−2+mx+2m)(x+2)<0
−2+mx+2m=0 dla x=0 więc
−2+2m=0 ⇒ m=1
Chciałem uniknąć metody graficznej w tym wypadku wiec.
(2−mx−2m)(x+2)>0
Funkcja musi wyglądac tak miejsa zerowe 0 i −2. −2 mam juz z głowy
−(2−mx−2m)(x+2)<0
(−2+mx+2m)(x+2)<0
−2+mx+2m=0 dla x=0 więc
−2+2m=0 ⇒ m=1