ostro
Ateusz: ostroslupy kąt do plaszczyzny
witam
jeśli jest ostrosłup czworokątny − jak będzie wyglądał kąt między − np. wysokością jednej ze
ścian bocznych a płaszczyzną podstawy?
jeśli jest ostrosłup trójkątny − −||−
28 lut 18:38
iteRacj@: ostrsłup prawidłowy czy dowolny?
28 lut 18:58
Ateusz: @iteRacj@
a będzie różnica?
w takim razie, może wszystkie po kolei...
28 lut 19:02
iteRacj@: Tak, bedzie.
Jeśli nikt nie odpowie wcześniej, to narysuję to za dwie godziny.
28 lut 19:06
Mila:
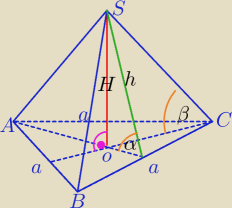
ABCS− ostrosłup prawidłowy trójkątny
α− kąt między ścianą boczną a płaszczyzną podstawy ( kąt między wysokością
ściany bocznej a jej rzutem prostokątnym na pł. podstawy )
β− kąt między krawędzią boczną a płaszczyzną podstawy ( kąt między krawędzią boczną
a jej rzutem prostokątnym na pł. podstawy )
28 lut 19:17
Ateusz: @Mila
w jaki sposób wyznaczamy spodek wysokości poszczególnych ostrosłupów?
a w szkole sorka cos mowila, ze wysokosc sciany bocznej musi stykac sie z punktem stycznosci
kola wpisanego w podstawe
jak z tym jest?
28 lut 19:28
Ateusz: *musi łączyć się z wierzchołkiem kąta prostego w punkcie styczności koła wpisanego w podstawę z
podstawą ściany, od której ta wysokość pochodzi
28 lut 19:35
Mila:
Spodek wysokości ostrosłupa.
1)
Jeżeli krawędzie boczne ostrosłupa są nachylone do podstawy pod takim samym kątem
do płaszczyzny podstawy , to spodek wysokości ostrosłupa leży w środku okręgu
opisanego na podstawie.
2)
Jeżeli krawędzie boczne ostrosłupa są tej samej długości ,
to spodek wysokości ostrosłupa leży w środku okręgu opisanego na podstawie.
3)
Jeżeli ściany boczne ostrosłupa są nachylone do podstawy pod takim samym kątem,
to spodek wysokości ostrosłupa leży w środku okręgu wpisanego w podstawę.
wę.
28 lut 20:16
Mila:
Ostrosłup trójkątny.
Spodek wysokości ściany bocznej znajduje się w punkcie styczności okręgu wpisanego
w trójkąt będący podstawą ostrosłupa.
W ostrosłupie prawidłowym trójkątnym ( jak na rysunku) punktem tym jest środek krawędzi
podstawy.
Wpisuj konkretne zadania, to się nauczysz.
28 lut 20:21
Ateusz: @Mila
wielkie dzięki

jak jeszcze czegos nie bede wiedzial, to pozwole sobie tutaj zawitac ponownie, do tego tematu
28 lut 20:25
Mila:
Poczekaj na
Iterację, robi piękne rysunki w Geogebrze.

28 lut 20:35
Ateusz: rysunki to też druga sprawa

srednio mi wychodzi sama konstrukcja, raz sie uda perfekcyjni ostroslup, a raz ( o wiele
czesciej) taki, ze sciany zaslaniaja sie nawzajem
trudno jest wyczuc kąty w podstawach
28 lut 20:44
Mila:
Na forum jest mnóstwo zadań z rysunkami.
wpisz w wyszukiwarkę hasło Ostrosłupy.
28 lut 20:48
iteRacj@:
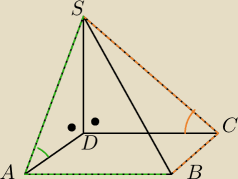
To ja dodam jeszcze ostrosłup czworokątny, który nie jest ostrosłupem prawidłowym. Jedna z
krawędzi bocznych jest prostopadła do podstawy, w podstawie jest prostokąt.
Kąty między wysokościami ścian bocznych a płaszczyzną podstawy:
SA − wysokość ściany bocznej SAB,
<SAD kąt między wysokością tej ściany a
płaszczyzną podstawy
SC − wysokość ściany bocznej SCB,
<SCD kąt między wysokością tej ściany a
płaszczyzną podstawy
SD − wysokość ściany bocznej SCD, <SDA=90
o kąt między wysokością tej ściany a płaszczyzną
podstawy
SD − wysokość ściany bocznej SAD, <SDC=90
o kąt między wysokością tej ściany a płaszczyzną
podstawy
28 lut 22:22
Ateusz: @iteRacj@
dzięki, ale czy na pewno opisy odcinków SA SC SD są poprawne?
potrzebuje pomocy :
podstawą ostroslupa jest trapez rownoramienny. krotsza podstawa i ramie tego trapezu sa tej
samej dlugosci. wszystkie krawedzie boczne ostroslupa maja dlugosc 61cm a wysokosc ostroslupa
do 60cm. wiedzac, ze srodek okregu opisanego na trapezie jest srodkiem dluzszej pdostawy
trapezu, oblicz pole tego trapezu.
1 mar 18:06
Ateusz: R=11, to wiem, ale co dalej?
mam 3 przystające trójkąty. każdy z nich równoramienny, każdy ma po 2 kąty alfa i jeden beta.
co w związku z tym?
1 mar 18:08
Ateusz: a wysokosc ostroslupa TO 60cm*
1 mar 18:10
Ateusz: Dobra, przypomniałem sobie o sumie miar kątów przeciwległych w czworokącie wpisanym w okrąg...

wyszło 3alfa=180
alfa=60
zatem trójkąty będą równoboczne, a pole to (R
2√3)/2
1 mar 18:13
Mila:
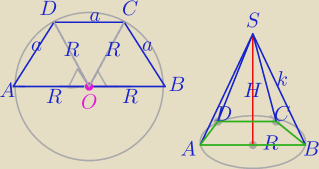
Podpowiedź:
W podstawie jest trapez równoramienny, dłuższa podstawa jest średnicą okręgu
opisanego na tym trapezie.
O− spodek wysokości ostrosłupa
k
2=R
2+H
2
1 mar 18:25
Ateusz: @Mila
to zadanie już zrobiłem, ale i tak dzięki

kolejne :
podstawąostrosłupa jest kwadrat, a spodek wysokości znajduje sie w jednym z wierzcholkow tego
kwadratu. wiedzac, ze wysokosc tego ostroslupa jest rowna krwaedzi podstawy, oblicz
a) miare kata nachylenia scian bocznych ktore nie zawieraja wysokosci ostroslupa, do
plaszczyzyny podstawy
1 mar 19:03
Ateusz: nie mam pojęcia gdzie będzie znajdował się kąt między wysokością ściany bocznej, a płaszczyzną
podstawy
1 mar 19:04
Ateusz: płaszczyzna w tym przypadku to po prostu któraś z krawędzi podstawy ?
w takim wypadku wysokość musiałaby zawierać się w krawędzi bocznej
tak będzie?
to by ujawnilo nam 2 kolejne trojkaty prostokatne
1 mar 19:14
Mila:
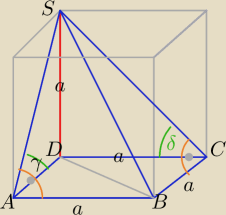
Najlepiej umieścić ten ostrosłup w sześcianie.
|SC|=a
√2=|SA|
|SB|
2=p
2+a
2=(a
√2)
2+a
2=3a
2
|SB|=a
√3
ΔBCS:
Boki: a, a
√2, a
√3
ΔBCS− Δprostokątny ( tw. odwrotne do tw. Pitagorasa)
Analogicznie :ΔBAS− Δprostokątny
SC jest wysokością w ΔBCS, jej rzutem prostokątnym na płaszczyznę ABCD jest DC
1 mar 20:27
Ateusz: @Mila
chodzilo mi wlasnie o to jedno potwierdzenie, ktore zawarlas w ostatnim zdaniu

tylko troche na odwrot − jesli dla wysokości sciany bocznej, jej rzutem prostokątnym na
plaszczyzne podstawy jest krawędź podstawy, to ta wysokość będzie jednocześnie krawędzią
boczną −−> ściana jest trójkątem prostokątnym
1 mar 20:30
Mila:
Tak, to oczywiste.
Zaznaczyłam kąty na zielono .
1 mar 20:34
Ateusz: @Mila
jeszcze pytanko −
28 lutego godzina 20:21 − gdy pisalas o spodku wysokosci sciany bocznej, ktory znajduje sie w
punkcie stycznosci, to pisalas o scianie bocznej wylacznie w ostroslupie, w ktorym wszystkie
sciany sa nachylone do podstawy pod tym samym kątem?
1 mar 21:50
Mila:
Jeżeli ostrosłup jest prawidłowy, to jest tak, jak piszesz.
W innych ostrosłupach , jeżeli ściany boczne są nachylone pod tym samym kątem ,
to też tak będzie .
Są ostrosłupy o podstawach w które nie można wpisać okręgu .
Wysokość ściany bocznej to wysokość trójkąta. Na rysunku 20:27 masz właśnie taki przykład,
że spodki wysokości nie pokrywają się z punktami stycznymi okręgu wpisanego w podstawę.
Z pewnością trafisz na taki ostrosłup.
1 mar 22:42
Ateusz: Czyli wysokość ściany bocznej zawsze ma spodek w miejscu styczności podstawy z okręgiem w nią
wpisanym, chyba że np. spodek wysokości znajduje się nad jednym z wierzchołków, lub podstawą
jest figura, której nie da się opisać na okręgu. Dobrze zrozumiałem?
Zatem jeśli podstawą jest trójkąt, a wiadomo że każdy trójkąt da się opisać na okręgu, i nie
jest określone, że spodek wysokości znajduje się nad wierzchołkiem, to wysokość ściany bocznej
takiego ostrosłupa będzie zawsze spadać na punkt styczności?
1 mar 22:52
Mila:
Wszystko zależy od rodzaju ostrosłupa . Analizujemy treść zadania.
Naprawdę , rozwiązuj zadania, to zrozumiesz problem.
Jak spodek wysokości może się znajdować nad wierzchołkiem? ?
To, że w podstawę można wpisać okrąg nie określa , gdzie leży spodek wysokości ściany bocznej.
20:16 masz napisane , jakie wnioski wyciągamy z treści tam podanej przed słowem "to".
1 mar 23:32
Mila:
Dobranoc

1 mar 23:32
Ateusz: Rozumiem
potrzebuje pomocy :
Podstawą ostroslupa jest trojkat rownoboczny o boku dlugosci a. jedna ze scian bocznych, bedaca
rowniez trojkatem rownobocznym jest prostopadla do plaszczyzny podstawy. oblicz pole
powierzchni bocznej ostroslupa
spodek wysokosci ostroslupa bedzie znajdowal sie w tym samym miejscu co spodek wysokosci sciany
bocznej (trojkata rownobocznego) ?
i co dalej ?
2 mar 21:57
Mila:
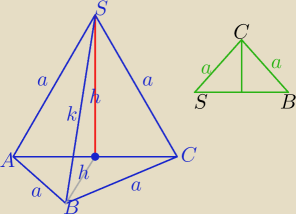
1) k
2=h
2+h
2=2h
2
2)ΔABS≡ΔBCS − trójkąty równoramienne o podstawie k i ramionach równych a.
Wysokość:
| | √5 | | √5 | | a√10 | |
x= |
| a= |
| a= |
| |
| | √8 | | 2√2 | | 4 | |
| | 1 | | a√6 | | a√10 | |
3)PSBC= |
| * |
| * |
| |
| | 2 | | 2 | | 4 | |
dokończ sam
2 mar 22:46
Ateusz:
dzieki po raz kolejny, nie ogarnalem, ze to dwie sciany to sa te same trojkaty o tej samej
podstawie, bo byly tak odwrocone o 90 stopni

w prostopadloscianie ABCDA
1B
1D
1C
1 podstawa ABCD jest kwadratem. wysokosc C
1E trojklata
BC
1D
1 dzieli przekatna D
1B na odcinki o dlugosci D
1E=2 EB=8 oblicz objetosc tego
prostopadloscianu
w ktorym miejscu trojkat BC1D1 ma kat prosty? bo jest prostokatny tak jak EC1D1, to wynika z
podobienstwa
2 mar 23:14
Ateusz: ABCDA1B1C1D1
2 mar 23:15
Mila:
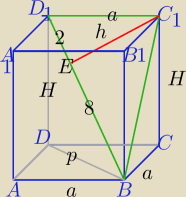
Do poprzedniego zadania: dobrze.
∡D
1C
1B− jest prosty.
D
1C
1 jest prostopadła do płaszczyzny BCC!B! to jest prostopadła do każdej prostej leżącej
w tej płaszczyźnie i przechodzącej przez punkt przebicia ( Czyli C1)
D
1C1⊥C
1C,
D
1C1⊥C
1B
2)
h jest poprowadzona z wierzchołka kąta prostego i dzieli przeciwprostokątną na odcinki 2 i 8⇔
h
2=2*8
h=4
resztę licz z tw. Pitagorasa.
2 mar 23:40
Mila:
Następne zadnia wpisuj w nowym wątku, bo trzeba długo przewijać stronkę.

2 mar 23:41
 ABCS− ostrosłup prawidłowy trójkątny
α− kąt między ścianą boczną a płaszczyzną podstawy ( kąt między wysokością
ściany bocznej a jej rzutem prostokątnym na pł. podstawy )
β− kąt między krawędzią boczną a płaszczyzną podstawy ( kąt między krawędzią boczną
a jej rzutem prostokątnym na pł. podstawy )
ABCS− ostrosłup prawidłowy trójkątny
α− kąt między ścianą boczną a płaszczyzną podstawy ( kąt między wysokością
ściany bocznej a jej rzutem prostokątnym na pł. podstawy )
β− kąt między krawędzią boczną a płaszczyzną podstawy ( kąt między krawędzią boczną
a jej rzutem prostokątnym na pł. podstawy )
 jak jeszcze czegos nie bede wiedzial, to pozwole sobie tutaj zawitac ponownie, do tego tematu
jak jeszcze czegos nie bede wiedzial, to pozwole sobie tutaj zawitac ponownie, do tego tematu

 srednio mi wychodzi sama konstrukcja, raz sie uda perfekcyjni ostroslup, a raz ( o wiele
czesciej) taki, ze sciany zaslaniaja sie nawzajem
trudno jest wyczuc kąty w podstawach
srednio mi wychodzi sama konstrukcja, raz sie uda perfekcyjni ostroslup, a raz ( o wiele
czesciej) taki, ze sciany zaslaniaja sie nawzajem
trudno jest wyczuc kąty w podstawach
 To ja dodam jeszcze ostrosłup czworokątny, który nie jest ostrosłupem prawidłowym. Jedna z
krawędzi bocznych jest prostopadła do podstawy, w podstawie jest prostokąt.
Kąty między wysokościami ścian bocznych a płaszczyzną podstawy:
SA − wysokość ściany bocznej SAB, <SAD kąt między wysokością tej ściany a
płaszczyzną podstawy
SC − wysokość ściany bocznej SCB, <SCD kąt między wysokością tej ściany a
płaszczyzną podstawy
SD − wysokość ściany bocznej SCD, <SDA=90o kąt między wysokością tej ściany a płaszczyzną
podstawy
SD − wysokość ściany bocznej SAD, <SDC=90o kąt między wysokością tej ściany a płaszczyzną
podstawy
To ja dodam jeszcze ostrosłup czworokątny, który nie jest ostrosłupem prawidłowym. Jedna z
krawędzi bocznych jest prostopadła do podstawy, w podstawie jest prostokąt.
Kąty między wysokościami ścian bocznych a płaszczyzną podstawy:
SA − wysokość ściany bocznej SAB, <SAD kąt między wysokością tej ściany a
płaszczyzną podstawy
SC − wysokość ściany bocznej SCB, <SCD kąt między wysokością tej ściany a
płaszczyzną podstawy
SD − wysokość ściany bocznej SCD, <SDA=90o kąt między wysokością tej ściany a płaszczyzną
podstawy
SD − wysokość ściany bocznej SAD, <SDC=90o kąt między wysokością tej ściany a płaszczyzną
podstawy
 wyszło 3alfa=180
alfa=60
zatem trójkąty będą równoboczne, a pole to (R2√3)/2
wyszło 3alfa=180
alfa=60
zatem trójkąty będą równoboczne, a pole to (R2√3)/2
 Podpowiedź:
W podstawie jest trapez równoramienny, dłuższa podstawa jest średnicą okręgu
opisanego na tym trapezie.
O− spodek wysokości ostrosłupa
k2=R2+H2
Podpowiedź:
W podstawie jest trapez równoramienny, dłuższa podstawa jest średnicą okręgu
opisanego na tym trapezie.
O− spodek wysokości ostrosłupa
k2=R2+H2
 kolejne :
podstawąostrosłupa jest kwadrat, a spodek wysokości znajduje sie w jednym z wierzcholkow tego
kwadratu. wiedzac, ze wysokosc tego ostroslupa jest rowna krwaedzi podstawy, oblicz
a) miare kata nachylenia scian bocznych ktore nie zawieraja wysokosci ostroslupa, do
plaszczyzyny podstawy
kolejne :
podstawąostrosłupa jest kwadrat, a spodek wysokości znajduje sie w jednym z wierzcholkow tego
kwadratu. wiedzac, ze wysokosc tego ostroslupa jest rowna krwaedzi podstawy, oblicz
a) miare kata nachylenia scian bocznych ktore nie zawieraja wysokosci ostroslupa, do
plaszczyzyny podstawy
 Najlepiej umieścić ten ostrosłup w sześcianie.
|SC|=a√2=|SA|
|SB|2=p2+a2=(a√2)2+a2=3a2
|SB|=a√3
ΔBCS:
Boki: a, a√2, a√3
ΔBCS− Δprostokątny ( tw. odwrotne do tw. Pitagorasa)
Analogicznie :ΔBAS− Δprostokątny
SC jest wysokością w ΔBCS, jej rzutem prostokątnym na płaszczyznę ABCD jest DC
Najlepiej umieścić ten ostrosłup w sześcianie.
|SC|=a√2=|SA|
|SB|2=p2+a2=(a√2)2+a2=3a2
|SB|=a√3
ΔBCS:
Boki: a, a√2, a√3
ΔBCS− Δprostokątny ( tw. odwrotne do tw. Pitagorasa)
Analogicznie :ΔBAS− Δprostokątny
SC jest wysokością w ΔBCS, jej rzutem prostokątnym na płaszczyznę ABCD jest DC
 tylko troche na odwrot − jesli dla wysokości sciany bocznej, jej rzutem prostokątnym na
plaszczyzne podstawy jest krawędź podstawy, to ta wysokość będzie jednocześnie krawędzią
boczną −−> ściana jest trójkątem prostokątnym
tylko troche na odwrot − jesli dla wysokości sciany bocznej, jej rzutem prostokątnym na
plaszczyzne podstawy jest krawędź podstawy, to ta wysokość będzie jednocześnie krawędzią
boczną −−> ściana jest trójkątem prostokątnym

 1) k2=h2+h2=2h2
1) k2=h2+h2=2h2
 w prostopadloscianie ABCDA1B1D1C1 podstawa ABCD jest kwadratem. wysokosc C1E trojklata
BC1D1 dzieli przekatna D1B na odcinki o dlugosci D1E=2 EB=8 oblicz objetosc tego
prostopadloscianu
w ktorym miejscu trojkat BC1D1 ma kat prosty? bo jest prostokatny tak jak EC1D1, to wynika z
podobienstwa
w prostopadloscianie ABCDA1B1D1C1 podstawa ABCD jest kwadratem. wysokosc C1E trojklata
BC1D1 dzieli przekatna D1B na odcinki o dlugosci D1E=2 EB=8 oblicz objetosc tego
prostopadloscianu
w ktorym miejscu trojkat BC1D1 ma kat prosty? bo jest prostokatny tak jak EC1D1, to wynika z
podobienstwa
 Do poprzedniego zadania: dobrze.
∡D1C1B− jest prosty.
D1C1 jest prostopadła do płaszczyzny BCC!B! to jest prostopadła do każdej prostej leżącej
w tej płaszczyźnie i przechodzącej przez punkt przebicia ( Czyli C1)
D1C1⊥C1C,
D1C1⊥C1B
2)
h jest poprowadzona z wierzchołka kąta prostego i dzieli przeciwprostokątną na odcinki 2 i 8⇔
h2=2*8
h=4
resztę licz z tw. Pitagorasa.
Do poprzedniego zadania: dobrze.
∡D1C1B− jest prosty.
D1C1 jest prostopadła do płaszczyzny BCC!B! to jest prostopadła do każdej prostej leżącej
w tej płaszczyźnie i przechodzącej przez punkt przebicia ( Czyli C1)
D1C1⊥C1C,
D1C1⊥C1B
2)
h jest poprowadzona z wierzchołka kąta prostego i dzieli przeciwprostokątną na odcinki 2 i 8⇔
h2=2*8
h=4
resztę licz z tw. Pitagorasa.
