matematykaszkolna.pl
Planimetria dowód Dango: W trójkącie ABC, w którym AB=c, BC=a i AC=b kąt BAC=2α.
 2 
Wykaż że sinα≤
, próbuję z tw, cosinusów ale daleko mi do rozwiązania
 2√bc 
27 lut 20:51
mat: a2=c2+b2−2cbcos2α a2=c2+b2−2cb(1−2sin2α) a2=c2+b2−2cb+4cbsin2α a2=(c−b)2+4cbsin2α a2≥4cbsin2α / bo (c−b)2≥0 więc
a2 
≥sin2α
4cb 
a 
≥sinα
2√cb 
27 lut 20:57
Mila: rysunek
 a 
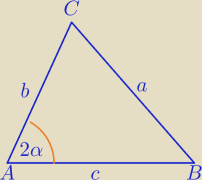
W trójkącie ABC, w którym AB=c, BC=a i AC=b kąt BAC=2α.Wykaż że sinα≤
 2√bc 
a2=b2+c2−2bc cos(2α)
 b2+c2−a2 
cos(2α)=
⇔
 2bc 
 b c a2 
cos(2α)=
+
−
 2c 2b 2bc 
 1 b c a2 
cos(2α)=
*(
+
)−
 2 c b 2bc 
 b c 
dla dodatnich b i c prawdziwa jest nierówność:(
+
)≥2
 c b 
 1 a2 
Zatem cos(2α)≥
*2−
 2 2bc 
a2 
≥1−cos(2α)
2bc 
a2 
≥1−1+2sin2α
2bc 
 a2 
sin2α≤
obie strony dodatnie
 4bc 
 a 
sinα≤
 2√bc 
==============
27 lut 23:23