Przedłużenia boków AD i BC czworokąta wypukłego ABCD przecinają się w punkcie S. Myszko: Przedłużenia boków AD i BC czworokąta wypukłego ABCD przecinają się w punkcie S. Wiedząc że |AD|=|SD|+5²₃,|SC|=24 cm,|BC|=36cm, wyznacz SD, tak aby czworokąt ABCD był trapezem

myszko: up

wredulus_pospolitus: sporo tych zadań z geometrii masz których ruszyć nie potrafisz

wredulus_pospolitus: wskazówka ... aby ABCD był trapezem to musi zajść AB || CD. w takim razie musi być spełnione tw. Talesa

Karolina: Czy ktoś wytłumaczy mi to zadanie? Bo mam takie same a widze że nie zostało rozwiązane. Również mam z nim problem

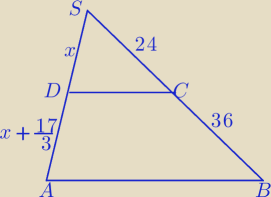
Mila: DC||AB jeżeli odpowiednie odcinki wyznaczone na ramionach kąta ASB są proporcjonalne (tw. odwrotne do tw. Talesa)

x		x+(17/3)
	=
24		36

	17
36x=24*(x+		)
	3

	34
x=
	3

Spr:

24		2
	=
36		3

34		34		17		34		2
	: (		+		)=		:17=		⇔
3		3		3		3		3

DC||AB ==========