W trójkąt prostokątny o przyprostokątnych 12 i 16 wpisano okra i na tym trójkąci
Myszko: W trójkąt prostokątny o przyprostokątnych 12 i 16 wpisano okra i na tym trójkącie opisano
okrąg. Oblicz odległość środków tych okręgów
26 lut 21:39
wredulus_pospolitus:
przyprostokątne 12 i 16 to przeciwprostokątna wynosi 20
Bo:
12 = 3*4
16 = 4*4
więc 20 = 5*4
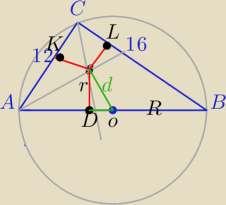
Rysunek
Zauważ, że środek opisanego jest w połowie przeciwprostokątnej
Znajdź wzór na promień okręgu wpisanego. Zbuduj trójkąt prostokątny, którego przeciwprostokątną
będzie szukana odległość pomiędzy środkami okręgów
26 lut 22:02
kapucyn: | | (a+b−c) | |
skoro wzorem jest r= |
| to promień wyjdzie ujemny, więc coś chyba nie tak |
| | 2 | |
26 lut 22:12
wredulus_pospolitus:
a to ciekaw jak Ci wyszła ujemna liczba licząc 12 + 16 − 20

26 lut 22:13
kapucyn: a przepraszam, źle oznaczyłem na moim rysunku i stąd te wnioski

26 lut 22:14
wredulus_pospolitus:
Nawet na chłopski rozum ... nierówność trójkąta mówi wprost: a+b − c > 0 dla dowolnego
'zestawu boków'

26 lut 22:16
Mila:
1)
|AB|
2=12
2+16
2
|AB|=20
R=10
| | 1 | | a+b+c | |
PΔ= |
| *12*16=96 i PΔ= |
| *r |
| | 2 | | 2 | |
| | 12+16+20 | |
96= |
| *r⇔ 96=24*r |
| | 2 | |
r=4
2)|KC|=4
|AK|=12−4=8=|AD|
|OD|=10−8=2
3)
W ΔSDO:
d
2=4
2+2
2=20
d=2
√5
==============
Wzór Eulera− odległość środka okręgu wpisanego w Δ od środka okręgu opisanego
d
2=R*(R−2r)
https://pl.wikipedia.org/wiki/Twierdzenie_Eulera_(geometria)
26 lut 22:42
kapucyn: Mila, wszystko rozumiem poza tym obliczeniem odcinka |OD|, czy możesz wytłumaczyć, bądź
ktokolwiek inny skąd wzięło się tam 10?
28 lut 19:08
kapucyn: a dobra, już wszystko wiem

to R.
28 lut 19:08
Mila: 
1 mar 18:07



 1)
|AB|2=122+162
|AB|=20
R=10
1)
|AB|2=122+162
|AB|=20
R=10
 to R.
to R.
